题目内容
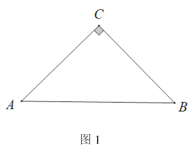
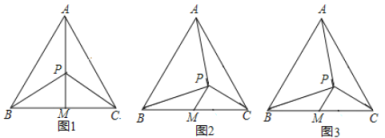
【题目】如图,△ABC中,E是AC上一点,且AE=AB,∠BAC=2∠EBC ,以AB为直径的⊙O交AC于点D,交EB于点F.
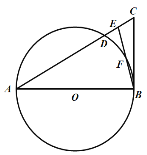
(1)求证:BC与⊙O相切;
(2)若AB=8,BE=4,求BC的长.
【答案】(1)证明见解析;(2)BC=![]()
【解析】
(1)运用切线的判定,只需要证明AB⊥BC即可,即证∠ABC=90°. 连接AF,依据直径所对圆周角为90度,可以得到∠AFB=90°,依据三线合一可以得到2∠BAF=∠BAC,再结合已知条件进行等量代换可得∠BAF=∠EBC,最后运用直角三角形两锐角互余及等量代换即可.
(2)依据三线合一可以得到BF的长度,继而算出∠BAF=∠EBC的正弦值,过E作EG⊥BC于点G,利用三角函数可以解除EG的值,依据垂直于同一直线的两直线平行,可得EG与AB平行,从而得到相似三角形,依据相似三角形的性质可以求出AC的长度,最后运用勾股定理求出BC的长度.
(1)证明:连接AF.
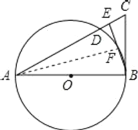
∵AB为直径, ∴∠AFB=90°.
又∵AE=AB,
∴2∠BAF=∠BAC,∠FAB+∠FBA=90°.
又∵∠BAC=2∠EBC,
∴∠BAF=∠EBC,
∴∠FAB+∠FBA=∠EBC+∠FBA=90°.
∴∠ABC=90°.即AB⊥BC,
∴BC与⊙O相切;
(2)解:过E作EG⊥BC于点G,
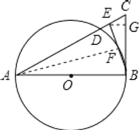
∵AB=AE,∠AFB=90°,
∴BF=![]() BE=
BE=![]() ×4=2,
×4=2,
∴sin∠BAF=![]() ,
,
又∵∠BAF=∠EBC,
∴sin∠EBC=![]() .
.
又∵在△EGB中,∠EGB=90°,
∴EG=BEsin∠EBC=4×![]() =1,
=1,
∵EG⊥BC,AB⊥BC,
∴EG∥AB,
∴△CEG∽△CAB,
∴![]() .
.
∴![]() ,
,
∴CE=![]() ,
,
∴AC=AE+CE=8+![]() =
=![]() .
.
在Rt△ABC中,
BC=![]()

 名师点睛字词句段篇系列答案
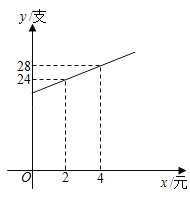
名师点睛字词句段篇系列答案【题目】小李经营的车饰店销售某品牌车漆修复液,已知其进价为40元/支,试销阶段发现将售价定为80元/支时,每天可销售20支,后来为了扩大销售量,小李适当降低了售价,销售量y(支)与降价x(元)的关系如图所示.
(1)请仔细读题,并补全下面表格:
降价x/元 | … | 2 | 4 |
| x | … |
销量y/支 | … | 24 | 28 | 30 |
| … |
(2)若要使得平均每天销售这种修复液的利润W最大,则每支修复液应该降价多少元?最大的利润W为多少元?