��Ŀ����
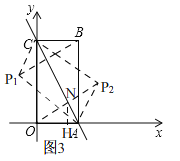
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�һ�κ���y=��2x+8��ͼ����x�ᣬy��ֱ��ڵ�A����C������A��AB��x�ᣬ����Ϊ��A������C��CB��y�ᣬ����Ϊ��C�����������ཻ�ڵ�B��

��1���߶�AB��BC��AC�ij��ֱ�ΪAB=�� ����BC=�� ����AC=�� ����
��2���۵�ͼ1�е���ABC��ʹ��A���C�غϣ��ٽ��۵����ͼ��չ�����ۺ�DE��AB�ڵ�D����AC�ڵ�E������CD����ͼ2��
�������A��B��������ѡһ��������ѡ���� ���⣮
A�������߶�AD�ij���
����y���ϣ��Ƿ���ڵ�P��ʹ����APDΪ���������Σ������ڣ���ֱ��д���������������е�P�����ꣻ�������ڣ���˵�����ɣ�
B�������߶�DE�ij���
��������ƽ���ڣ��Ƿ���ڵ�P������B�⣩��ʹ���Ե�A��P��CΪ���������������ABCȫ�ȣ������ڣ���ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��8��4��4![]() ����2��������.
����2��������.
�������������������1����ȷ����OA=4��OC=8�������ó�AB=8��BC=4�����ù��ɶ������ɵó�AC��
��2��A���������۵������ʵó�BD=8��AD������ù��ɶ������ɵó�������
�ڷ�����������÷��̵�˼�뼴�ɵó�������
B���������۵������ʵó�AE�����ù��ɶ������ɵó�������
�����жϳ���APC=90�㣬�ٷ�������ۼ��㼴�ɣ�
���������������1����һ�κ���y=��2x+8��ͼ����x����y��ֱ��ڵ�A����C����A��4��0����C��0��8������OA=4��OC=8����AB��x����CB��y������AOC=90�㣬���ı���OABC�Ǿ�������AB=OC=8��BC=OA=4����Rt��ABC�������ݹ��ɶ�������AC=![]() =4
=4![]() ���ʴ�Ϊ��8��4��4
���ʴ�Ϊ��8��4��4![]() ��
��
��2��ѡA�����ɣ�1��֪��BC=4��AB=8�����۵�֪��CD=AD����Rt��BCD����BD=AB��AD=8��AD�����ݹ��ɶ�������CD2=BC2+BD2������AD2=16+��8��AD��2����AD=5��
���ɢ�֪��D��4��5������P��0��y������A��4��0������AP2=16+y2��DP2=16+��y��5��2���ߡ�APDΪ�������������������������ۣ�
����AP=AD����16+y2=25����y=��3����P��0��3����0����3����
����AP=DP����16+y2=16+��y��5��2����y=![]() ����P��0��
����P��0��![]() ����
����
����AD=DP��25=16+��y��5��2����y=2��8����P��0��2����0��8����
����������P��0��3����0����3����P��0��![]() ����P��0��2����0��8����
����P��0��2����0��8����
ѡB������A��֪��AD=5�����۵�֪��AE=![]() AC=2
AC=2![]() ��DE��AC��E����Rt��ADE����DE=
��DE��AC��E����Rt��ADE����DE=![]() =
=![]() ��
��
�ڡ��Ե�A��P��CΪ��������������ABCȫ�������APC�ա�ABC�����CPA�ա�ABC�����APC=��ABC=90�㣮���ı���OABC�Ǿ��������ACO�ա�CAB����ʱ��������������P�͵�O�غ�������P��0��0����
��ͼ3������O��ON��AC��N����֤����AON�ס�ACO����![]() ����
����![]() ����AN=
����AN=![]() ������N��NH��OA����NH��OA�����ANH�ס�ACO����
������N��NH��OA����NH��OA�����ANH�ס�ACO����![]() ����
����![]() ����NH=
����NH=![]() ��AH=
��AH=![]() ����OH=
����OH=![]() ����N��
����N��![]() ��������P2���O����AC�Գ�����P2��
��������P2���O����AC�Գ�����P2��![]() ����ͬ������B����AC�ĶԳƵ�P1��ͬ�ϵķ�������P1����
����ͬ������B����AC�ĶԳƵ�P1��ͬ�ϵķ�������P1����![]() ����
����
�������������������ĵ�P������Ϊ����0��0������![]() ��������
��������![]() ����
����

 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�