题目内容
【题目】定义:对于函数y,我们称函数叫做函数|y|的正值函数.例如:函数y![]() 的正值函数为y=|
的正值函数为y=|![]() |.
|.
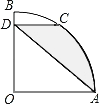
如图,曲线y![]() (x>0)请你在图中画出y=x+3的正值函数的图象.
(x>0)请你在图中画出y=x+3的正值函数的图象.
(1)写出y=x+3的正值函数的两条性质;
(2)y=x+3的正值函数的图象与x轴、y轴、曲线y![]() (x>0)的交点分别是A,B,C.点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与正值函数图象交于另一点E,与曲线交于点P.
(x>0)的交点分别是A,B,C.点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与正值函数图象交于另一点E,与曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
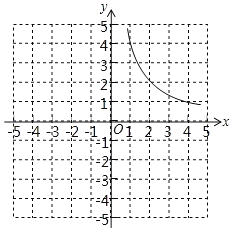
【答案】(1)①图象与x轴交于(﹣3,0),②当x<﹣3时,y随x的增大而减小;(2)①m![]() 时,△PAD的面积最大,最大值为
时,△PAD的面积最大,最大值为![]() ;②能,D(﹣1,2).
;②能,D(﹣1,2).
【解析】
(1)利用描点法画出y=x+3的正值函数为y=|x+3|的图形即可;
(2)①设D(m,m+3),则P(![]() ,m+3),利用三角形的面积公式构建二次函数,利用二次函数的性质解决问题即可;
,m+3),利用三角形的面积公式构建二次函数,利用二次函数的性质解决问题即可;
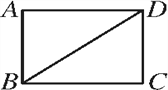
②如图2中,连接EC.假设四边形APCE是平行四边形,则AD=CD,求出点E,P的坐标,再验证是不是平行四边形即可.
(1)y=x+3的正值函数为y=|x+3|,函数图象如图所示:
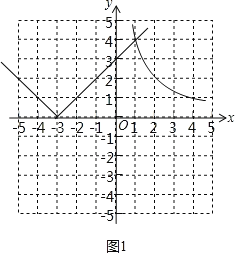
函数y=|x+3|的性质:①图象与x轴交于(﹣3,0).
②当x<﹣3时,y随x的增大而减小.
③当x>﹣3时,y随x的增大而增大.
(2)①如图2中,
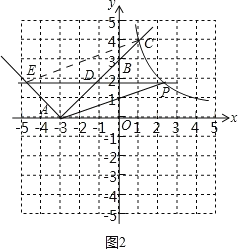
设D(m,m+3),则P(![]() ,m+3),
,m+3),
∴PD![]() m
m![]() ,
,
∴S△APD![]() (
(![]() )(m+3)
)(m+3)![]() (m2+3m﹣4)
(m2+3m﹣4)![]() (m
(m![]() )2
)2![]() ,
,
∵![]() 0,
0,
∴m![]() 时,△PAD的面积最大,最大值为
时,△PAD的面积最大,最大值为![]() .
.
②如图2中,连接EC.假设四边形APCE是平行四边形,则AD=CD.
∵A(﹣3,0),C(1,4),
∴D(﹣1,2),
∴P(2,2),E(﹣5,2),
∴DE=DP=3.
∵DE=DP,AD=DC,
∴四边形APCE是平行四边形,符合条件.
【点晴】
考查了反比例函数的性质、平行四边形的判定和性质等知识,解题的关键是理解题意,学会利用参数构建二次函数解决最值问题.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】为了防范疫情,顺利复学,某市教育局决定从甲、乙两地用汽车向![]() 两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,
两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,![]() 两校分别需要口罩30万个,20万个,两地到
两校分别需要口罩30万个,20万个,两地到![]() 两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
路程 | 路程 | |
甲地 | 乙地 | |
A校 | 10 | 20 |
B校 | 15 | 15 |
(1)根据题意,在答题卡中填写下表:
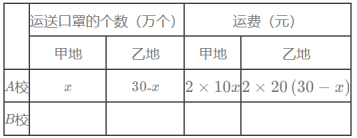
(2)设总运费为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?
的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?