题目内容
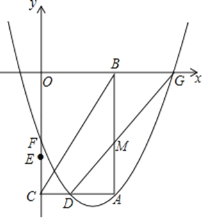
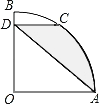
【题目】如图，在扇形AOB中，∠AOB＝90°，点C在
，
，OA＝3，CD⊥OB于点D，则图中阴影部分的面积为_____．
【答案】
π﹣
．
【解析】
连接OC，AC，如图，由点C为
的三等分点可得∠COD＝30°，∠AOC＝60°，由CD⊥OB可得CD∥OA，进而可得S△OCD＝S△ACD，解直角△OCD即可求出CD与OD的长，然后利用阴影部分的面积＝S△ACD+S扇形AOC－S△AOC代入数据计算即可．
解：连接OC，AC，如图，
∵点C为的三等分点，∠AOB＝90°，
∴∠COD＝30°，∠AOC＝60°，
∵CD⊥OB，∴CD∥OA，
∴S△OCD＝S△ACD，
∵∠CDO＝90°，∠DOC＝30°，OC＝OA＝3，
∴CD＝，OD＝
，
∴图中阴影部分的面积＝S△ACD+S扇形AOC－S△AOC＝
＝
，
故答案为：．
练习册系列答案
相关题目
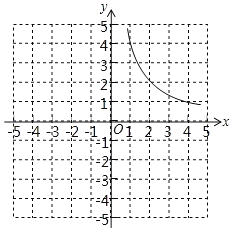
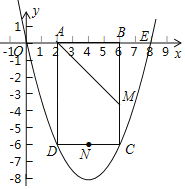
【题目】某兴趣小组对函数y＝
的图象和性质进行探究，请你帮助解决下面问题：
（1）函数y＝中自变量x的取值范围是 ；
（2）如表是x、y的几组对应值，则m＝ ；
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
（3）如图，已经画出了该函数图象的一部分，请你画出函数图象的另一部分；
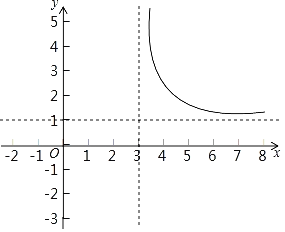
（4）该函数图象两个分支关于一个点成中心对称，这个点的坐标是 ；
（5）若函数y＝的图象上有三点A（x1，y1）、B（x2，y2）、C（x3，y3）且x1＜x2＜3＜x3，则y1、y2、y3的大小关系是 （用“＜”连接）．
