题目内容
【题目】在一个不透明的口袋里，装有若干个完全相同的A、B、C三种球，其中A球x个，B球x个，C球（x+1）个．若从中任意摸出一个球是A球的概率为0.25．
（1）这个袋中A、B、C三种球各多少个？
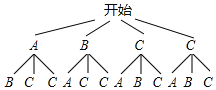
（2）若小明从口袋中随机模出1个球后不放回，再随机摸出1个．请你用画树状图的方法求小明摸到1个A球和1个C球的概率．
【答案】（1）这个袋中A、B、C三种球分别为1个、1个、2个；（2）
【解析】
（1）由题意列方程，解方程即可；
（2）首先画树状图，由概率公式即可得出答案．
解：由题意得：
[x+x+（x+1）]＝x，
解得：x＝1，∴x+1＝2，
答：这个袋中A、B、C三种球分别为1个、1个、2个；
（2）由题意，画树状图如图所示共有12个等可能的结果，摸到1个A球和1个C球的结果有4个，
∴摸到1个A球和1个C球的概率为
．
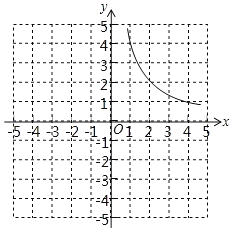
【题目】某兴趣小组对函数y＝
的图象和性质进行探究，请你帮助解决下面问题：
（1）函数y＝中自变量x的取值范围是 ；
（2）如表是x、y的几组对应值，则m＝ ；
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
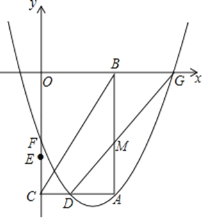
（3）如图，已经画出了该函数图象的一部分，请你画出函数图象的另一部分；
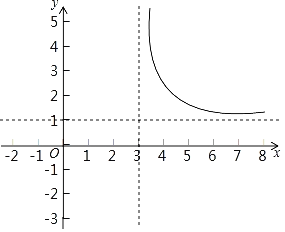
（4）该函数图象两个分支关于一个点成中心对称，这个点的坐标是 ；
（5）若函数y＝的图象上有三点A（x1，y1）、B（x2，y2）、C（x3，y3）且x1＜x2＜3＜x3，则y1、y2、y3的大小关系是 （用“＜”连接）．
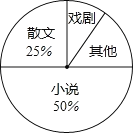
【题目】东营市某学校九年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别，每位同学仅选一项，根据调查结果绘制了不完整的频数分布表和扇形统计图．根据图表提供的信息，回答下列问题：
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | n |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | m | 1 |
（1）计算m= ，n= ．
（2）在扇形统计图中，“其他”类所在的扇形圆心角为 ；
（3）这个学校共有1000人，则读了戏剧类书籍的学生大约有多少人？
（4）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从中任意选出2名同学参加学校的戏剧社团，请用画树状图或列表的方法，求选取的2人恰好是乙和丙的概率．
