题目内容
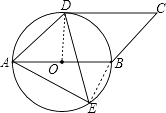
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°. 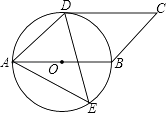
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE= ![]() ,求AE的值.
,求AE的值.
【答案】
(1)解:CD与圆O相切.
证明:连接OD,则∠AOD=2∠AED=2×45°=90°.
∵四边形ABCD是平行四边形,
∴AB∥DC.
∴∠CDO=∠AOD=90°.
∴OD⊥CD.
∴CD与圆O相切
(2)解:连接BE,则∠ADE=∠ABE.
∴sin∠ADE=sin∠ABE= ![]() .
.
∵AB是圆O的直径,
∴∠AEB=90°,AB=2×3=6.
在Rt△ABE中,sin∠ABE= ![]() =
= ![]() .
.
∴AE=5.

【解析】(1)连接OD,则∠AOD=为直角,由四边形ABCD是平行四边形,则AB∥DC.从而得出∠CDO=90°,即可证出答案.(2)连接BE,则∠ADE=∠ABE根据题意得sin∠ABE= ![]() .由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
.由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

【题目】某校需要招聘一名教师,对三名应聘者进行了三项素质测试![]() 下面是三名应聘者的综合测试成绩:
下面是三名应聘者的综合测试成绩:
应聘者 成绩 项目 | A | B | C |
基本素质 | 70 | 65 | 75 |
专业知识 | 65 | 55 | 50 |
教学能力 | 80 | 85 | 85 |
(1)如果根据三项测试的平均成绩确定录用教师,那么谁将被录用?
(2)学校根据需要,对基本素质、专业知识、教学能力的要求不同,决定按2:1:3的比例确定其重要性,那么哪一位会被录用?
【题目】如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上第一行的数是1,第二行的数是13,第三行的数是43,…,依此规律,第五行的数是( )

A. 183 B. 157 C. 133 D. 91
【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?