题目内容
【题目】如图,已知∠1和∠2互为补角,∠A=∠D.求证:AB∥CD.
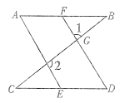
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(______).
又∠1和∠2互为补角(已知),
∴∠CGD和∠2互为补角,
∴AE∥FD(_________),
∴∠A=∠BFD(_______).
∵∠A=∠D(已知),
∴∠BFD=∠D(_______),
AB∥CD(______).
【答案】对顶角相等; 同旁内角互补,两直线平行; 两直线平行,同位角相等; 等量代换; 内错角相等,两直线平行.
【解析】
求出∠CGD和∠2互为补角,根据平行线的判定得出AE∥DF,根据平行线的性质得出∠AEC=∠D,求出∠AEC=∠A,根据平行线的判定即可得出结论.
∵∠1与∠CGD是对顶角,∴∠1=∠CGD(对顶角相等).
又∠1和∠2互为补角(已知),∴∠CGD和∠2互为补角,∴AE∥FD(同旁内角互补,两直线平行),∴∠A=∠BFD(两直线平行,同位角相等).
∵∠A=∠D(已知),∴∠BFD=∠D(等量代换),∴AB∥CD(内错角相等,两直线平行).
故答案为:对顶角相等;同旁内角互补,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.

【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
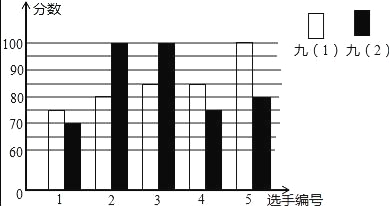
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) |
九(1) | 85 | |
九(2) | 100 |
(2)通过计算得知九(2)班的平均成绩为85分,请计算九(1)班的平均成绩.
(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.
(4)已知九(1)班复赛成绩的方差是70,请计算九(2)班的复赛成绩的方差,并说明哪个班的成绩比较稳定?