题目内容
【题目】如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,下面四个结论:①∠ABE=∠BAD;②△CEB≌△ADC;③AB=CE;④AD-BE=DE.其中正确的是 (将你认为正确结论的序号都写上).
【答案】①②④
【解析】解: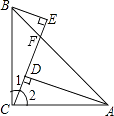
∵BE⊥CE于点E,AD⊥CE于点D ,
∴ ∠BEF=∠ADF=90°,
又∵∠BFE=∠AFD
∴∠ABE=∠BAD ;故 ① 正确
∵∠1+∠2=90° ,∠2+∠CAD=90°
∴∠1=∠CAD ,
又∠E=∠ADC=90°,AC=BC
∴△CEB≌△ADC (AAS), 故 ②正确
∴CE=AD,BE=CD
∴AD-BE=DE , 故 ④ 正确;
而③不能证明,
故答案为 :①、②、④
根据垂直的定义得出∠BEF=∠ADF=90° ,根据等顶角相等及三角形的内角和得出∠ABE=∠BAD ;故 ① 正确 ;根据同角的余角相等得出∠1=∠CAD ,从而利用AQAS判断出△CEB≌△ADC ,故 ②正确;根据全等三角形对应边相等得出CE=AD,BE=CD ,根据等式的性质得出AD-BE=DE , 故 ④ 正确; 从而得出答案。

练习册系列答案
相关题目