题目内容
【题目】为鼓励大众创业，万众创新，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数：y=﹣10x+500．
（1）李明在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元？
（2）设李明获得的利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（3）物价部门规定，这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元？
【答案】(1)承担总差价为600元(2) x=30时，W有最大值4000(3)政府为他承担总差价最少为250（12－10）=500元
【解析】试题分析：（1）把x=20代入y=-10x+500求出销售的件数，然后求出政府承担的成本价与出厂价之间的差价；
（2）由利润=销售价-成本价，得w=（x-10）（-10x+500），把函数转化成顶点坐标式，根据二次函数的性质求出最大利润；
（3）令-10x2+600x-5000=3000，求出x的值，结合图象求出利润的范围，然后设设政府每个月为他承担的总差价为p元，根据一次函数的性质求出总差价的最小值．
试题解析：(1) 在y=－10x+500中，x=20 y=300
300（12－10）=600 承担总差价为600元
(2) W=（－10x+500）(x－10)=－10(x－30)
+4000
x=30时，W有最大值4000
(3) W=－10(x－30)+4000 令W≥3000
画出草图，
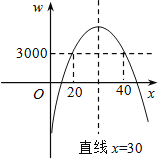
由图像可知
有20≤x≤40 ∵x≤25
∴20≤x≤25
在y=－10x+500中，－10＜0 ∴y随x的增大而减小
∴x=25时，y最小为250
∴政府为他承担总差价最少为250（12－10）=500元
