题目内容
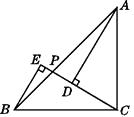
【题目】如图,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中,正确的有( )
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解:①∵BE⊥AC,AD⊥BC
∴∠AEH=∠ADB=90°
∵∠HBD+∠BHD=90°,∠EAH+∠AHE=90°,∠BHD=∠AHE
∴∠HBD=∠EAH
又∵DH=DC
∴△BDH≌△ADC(AAS)
∴BD=AD,BH=AC ;从而得出①③符合题意;
②:∵BC=AC
∴∠BAC=∠ABC
∵由①知,在Rt△ABD中,BD=AD
∴∠ABC=45°
∴∠BAC=45°
∴∠ACB=90°
∵∠ACB+∠DAC=90°,∠ACB<90°
②不符合题意;
解④:∵CE=CD ,∠ACB=∠ACB,∠ADC=∠BEC=90°,
∴△BEC≌△ADC
由于缺乏条件,无法证得△BEC≌△ADC
④不符合题意;
故应选:B.
根据垂直的定义得出∠AEH=∠ADB=90°,根据等顶角相等及等角的余角相等得出∠HBD=∠EAH,又DH=DC,从而利用AAS判断出△BDH≌△ADC,根据全等三角形对应边相等得出BD=AD,BH=AC ;根据等边对等角得出∠BAC=∠ABC,由等腰直角三角形的性质得出∠ABC=45°,根据等量代换得出∠BAC=45°,根据三角形的内角和得出∠ACB=90°,又∠ACB+∠DAC=90°,∠ACB<90°,从而得出②不符合题意;由于缺乏条件,无法证得△BEC≌△ADC,而要得出CE=CD,必须△BEC≌△ADC,故④不符合题意。

练习册系列答案
相关题目