题目内容
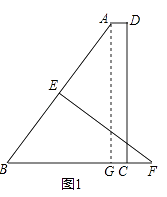
【题目】如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BC= ![]() ,AD=
,AD= ![]() ,CD=12,过AB的中点E作AB的垂线交BC的延长线于F.
,CD=12,过AB的中点E作AB的垂线交BC的延长线于F. 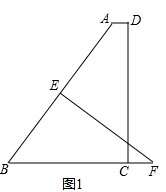
(1)求BF的长;
(2)如图2,以点C为原点,建立平面直角坐标系,请通过计算判断,过E点的反比例函数图象与直线AB是否还有另一个交点? 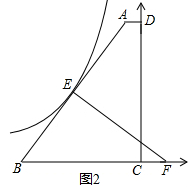
【答案】
(1)解:作AG⊥BC于G,则AG=CD=12,BG=BC﹣AD=9,
在Rt△ABG中,AB= ![]() =15,
=15,
∴BE= ![]() AB=
AB= ![]() .
.
∵∠ABG=∠FBE,∠AGB=∠FEB,
∴△ABG∽△FBE,
∴ ![]() =
= ![]() ,
,
得BF= ![]() =
= ![]()
(2)解:作EH⊥BC于H,则EH=6,
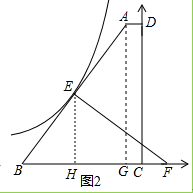
∴CH=6,
点E的坐标是(﹣6,6),
点B的坐标是(﹣ ![]() ,0),
,0),
设直线AB的解析式为y=kx+b,则 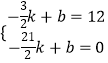
解得: 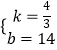 ,
,
∴直线AB的解析式为y= ![]() x+14.
x+14.
设反比例函数的解析式为y= ![]() ,
,
将E点坐标代入得,k1=﹣36.
∴过E点的反比例函数解析式为y=﹣ ![]() .
.
由﹣ ![]() =
= ![]() x+14,
x+14,
解得:x1=﹣6,x2=﹣ ![]() .
.
∴过E点的反比例函数图象与直线AB还有另一个交点
【解析】(1)作AG⊥BC于G,在直角△AG中利用勾股定理求得AB的长,然后证明△ABG∽△FBE,利用相似三角形的性质求解;(2)作EH⊥BC于H,求得直线AB的解析式,然后解反比例函数和一次函数的解析式组成的方程组求解.
【考点精析】本题主要考查了直角梯形和相似三角形的判定与性质的相关知识点,需要掌握一腰垂直于底的梯形是直角梯形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

练习册系列答案
相关题目