题目内容
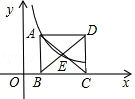
【题目】如图，抛物线y=ax2﹣ 
x﹣2（a≠）的图象与x轴交于A、B两点，与y轴交于C点，已知B点坐标为（4，0）．
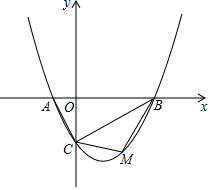
（1）求抛物线的解析式；
（2）若点M是线段BC下方的抛物线上一点，求△MBC的面积的最大值，并求出此时M点的坐标；
（3）试探究：△ABC的外接圆的圆心位置，并求出圆心坐标．
【答案】
（1）
解：将B（4，0）代入抛物线的解析式中，得：
0=16a﹣ 
×4﹣2，即：a= 
；
∴抛物线的解析式为：y= x2﹣ x﹣2
（2）
解：可得：B（4，0）、C（0，﹣2），设直线BC的解析式为：y=kx+b，
则 
，
解得： 
故直线BC的解析式为：y=x﹣2；
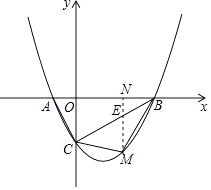
设xM=t，则yM= t2﹣ t﹣2，yN= t﹣2，
S△MBC=S△CME+S△BEM= EMON+ EMBN= EMOB
= （ t﹣2﹣ t2+ t+2）×4
=﹣t2+4t
=﹣（t﹣2）2+4，
∴当t=2时，S△MBC=最大值为4，此时M（2，﹣3）
（3）
解：由（1）的函数解析式可求得：A（﹣1，0）、C（0，﹣2）；
∴OA=1，OC=2，OB=4，
即：OC2=OAOB，
又∵OC⊥AB，
∴△OAC∽△OCB，
∴∠OCA=∠OBC；
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°，
∴△ABC为直角三角形，AB为△ABC外接圆的直径；
∴该外接圆的圆心为AB的中点，且坐标为（1.5，0）．
【解析】（1）该函数解析式只有一个待定系数，只需将B点坐标代入解析式中即可．（2）利用过点M作y轴的平行线，再利用S△MBC=S△CME+S△BEM得出二次函数最值得出答案；（3）首先根据抛物线的解析式确定A点坐标，然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置，由此确定圆心坐标．
【考点精析】本题主要考查了确定一次函数的表达式和二次函数的最值的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a才能正确解答此题．
