题目内容
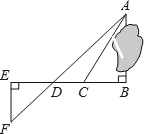
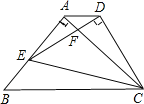
【题目】 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为![]() ,其中正确的是______________.
,其中正确的是______________.
【答案】②④⑤
【解析】
由三角形ABC与三角形ECD都为等腰直角三角形,利用等腰直角三角形的性质得到AB=AC,CD=DE,且四个锐角为45°,利用等式的性质得到∠BCE=∠ACD,故选项②正确;根据B与E重合时,A与D重合,此时DE与AC垂直;当B,E不重合时,A,D也不重合,根据∠BAC与∠EDC都为直角,判断∠AFE与∠DFC是否锐角,即可对于选项①做出判断;由两边对应成比例且夹角相等的三角形相似得到三角形BEC与三角形ADC相似,利用相似三角形对应角相等及等式的性质得到一对内错角相等,利用内错角相等两直线平行得到AD与BC平行,可得出选项④正确;由④的结论判断选项③即可;根据△ABC的面积为定值,若梯形ABCD的面积最大,则△ACD的面积最大;由高一定,面积最大即为AD最长,故梯形ABCD面积最大时,E、A重合,求出此时面积,即为最大面积,即可对于选项⑤做出判断.
∵△ABC,△ECD都为等腰直角三角形,
∴![]()
∴∠ACB∠ACE=∠DCE∠ACE,即∠BCE=∠ACD,故选项②正确;
当B,E重合时,A,D重合,此时DE⊥AC;
当B,E不重合时,A,D也不重合,由∠BAC与∠EDC都为直角,得到∠AFE与∠DFC必为锐角,故①错误;
④∵![]()
∴![]()
由①知∠ECB=∠DCA,
∴△BEC∽△ADC;
∴![]()
∴![]() ,即AD∥BC,故④正确;
,即AD∥BC,故④正确;
③∵由④知![]()
∴![]()
∵![]()
∴![]() ,即∠BEC<∠EAD;
,即∠BEC<∠EAD;
∴△EAD与△BEC不相似,故③错误;
⑤∵△ABC的面积为定值,
∴若梯形ABCD的面积最大,则△ACD的面积最大;
∵△ACD中,AD边上的高为定值,
∴若△ACD的面积最大,则AD的长最大;
由④的△BEC∽△ADC知:当AD最长时,BE也最长;
故梯形ABCD面积最大时,E、A重合,此时![]()
故S梯形ABCD=![]() ,故⑤正确.
,故⑤正确.
故答案为:②④⑤.

【题目】运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=![]() ;③足球被踢出9.5s时落地:④足球被踢出7.5s时,距离地面的高度是11.25m,其中不正确结论的个数是( )
;③足球被踢出9.5s时落地:④足球被踢出7.5s时,距离地面的高度是11.25m,其中不正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4