题目内容
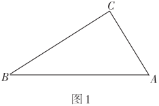
【题目】图形的折叠即图形的翻折或者说是对称变换.这类问题与生活紧密联系,内容丰富,解法灵活,具有开放性,可以培养我们的动手能力,空间想象能力和几何变换的思想.在综合与实践课上,每个小组剪了一些如图1所示的直角三角形纸片(![]() ,
,![]() ,
,![]() ),并将
),并将![]() 纸片中的各内角进行折叠操作:
纸片中的各内角进行折叠操作:
(1)如图2,“奋斗”小组将![]() 纸片中的
纸片中的![]() 进行折叠,使直角边
进行折叠,使直角边![]() 落在斜边
落在斜边![]() 上,点
上,点![]() 落在点
落在点![]() 位置,折痕为
位置,折痕为![]() ,则
,则![]() 的长为______
的长为______![]() .
.

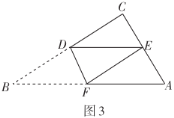
(2)如图3,“勤奋”小组将![]() 中的
中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 中点
中点![]() 上,折痕为
上,折痕为![]() ,则
,则![]() 的长为______
的长为______![]() .
.
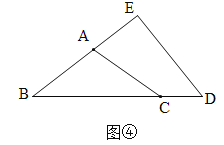
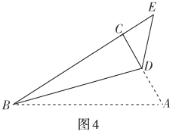
(3)如图4,“雄鹰”小组将![]() 纸片中的
纸片中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 延长线上的点
延长线上的点![]() 处,折痕为
处,折痕为![]() ,求出
,求出![]() 的长.
的长.
【答案】(1)3;(2)![]() ;(3)
;(3)![]() 长为
长为![]() .
.
【解析】
(1)设CD为xcm,则BD=BC-CD=(8-x)cm,利用折叠的性质表示出DE、BE,在Rt△BDE中,利用勾股定理得![]() ,得到一个关于x的方程,解出即可.
,得到一个关于x的方程,解出即可.
(2)设BD为ycm,则CD=BC-BD=(8-y)cm. 利用折叠的性质表示出DE、CE、DE,在Rt△CDE中,![]() ,得到一个关于y的方程,解出即可.
,得到一个关于y的方程,解出即可.
(3)在![]() 中,利用勾股定理求AB,进而利用折叠的性质求BE,CE,设
中,利用勾股定理求AB,进而利用折叠的性质求BE,CE,设![]() ,则
,则![]() ,
,![]() ,在
,在![]() 中,根据勾股定理得
中,根据勾股定理得![]() ,
,
可得![]() ,解出即可.
,解出即可.
解:(1)设CD为xcm,则BD=BC-CD=(8-x)cm.
∵![]() 纸片中的
纸片中的![]() 进行折叠,使直角边
进行折叠,使直角边![]() 落在斜边
落在斜边![]() 上,点
上,点![]() 落在点
落在点![]() 位置
位置
∴DE=CD=xcm,AE=AC=6cm,BE=AB-AE=10-6=4cm
∴在Rt△BDE中,利用勾股定理得![]()
![]()
解得x=3cm
(2)设BD为ycm,则CD=BC-BD=(8-y)cm.
∵![]() 中的
中的![]() 进行折叠,使点
进行折叠,使点![]() 落在直角边
落在直角边![]() 中点
中点![]() 上,折痕为
上,折痕为![]()
∴DE=BD=ycm,CE=![]() =6cm
=6cm
∴在Rt△CDE中,利用勾股定理得![]()
![]()
解得y=![]() cm
cm
(3)在![]() 中,
中,
![]() ,
,
根据折叠的性质可知:![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,根据勾股定理得
中,根据勾股定理得
![]() ,
,
即![]() ,
,
解得![]() ,
,
即![]() 长为
长为![]() .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:

(1)根据图中提供的数据列出如下统计表:
平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
王华 | 80 | b | 80 | d |
张伟 | a | 85 | c | 260 |
则a= ,b= ,c= ,d= ,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?