题目内容
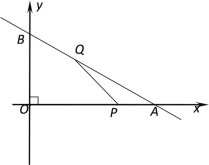
【题目】如图,已知直线l的函数表达式为y=![]() x+6,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
x+6,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
(1)求点A、B的坐标
(2)当以点A、P、Q为顶点的三角形是等腰三角形时,求时间t的值.
【答案】(1)A(8,0) B(0,6);(2)![]() ,
,![]() ,
,![]()
【解析】
(1)根据自变量与函数值的对应关系,可得相应的函数值,相应自变量的值;
(2)根据相似三角形的性质,可得关于t的方程,根据解方程,可得答案.
(1)∵直线的表达式为y=![]() x+6,
x+6,
令x=0,得y=6,
∴B(0,6),
令y=0,得0=![]() x+6,
x+6,
∴x=8,
∴ A(8,0) ;
(2)∵∠BOA=90°,
BO=6,AO=8,
∴AC=10,
由题意可知BQ=2t,AQ=10-2t,AP=t,
①当AQ=AP时,10-2t=t,
∴![]() ;
;
②当PQ=AP时,
过点P作PH⊥AQ,

∵PH⊥AQ,
∴∠PHA=∠AOB=90°,
∵∠HAP=∠OAB,
∴△AHP∽△AOB,
∴![]() ,
,
∵PQ=PA,PH⊥AQ,
∴AH=HQ,
∴AH=5-t,
∴![]() ,
,
∴![]() ;
;
③当QP=QA时,
过点Q作QH⊥AP,
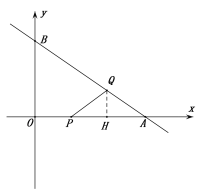
∵QH⊥AP,
∴∠QHA=∠AOB=90°,
∵∠QAH=∠BAO,
∴△AQH∽△ABO,
∴![]() ,
,
∵QP=QA,QH⊥AP,
∴AH=PH,
∴AH=![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述当![]() ,
,![]() ,
,![]() 时,以点A、P、Q为顶点的三角形是等腰三角形.
时,以点A、P、Q为顶点的三角形是等腰三角形.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .