��Ŀ����
����Ŀ����������ΰ��λͬѧ�ֱ��Լ�10����ѧ���Ҽ��ijɼ����Ƴ�����ͳ��ͼ��

��1������ͼ���ṩ�������г�����ͳ�Ʊ���
ƽ���ɼ����֣� | ��λ�����֣� | �������֣� | ���S2�� | |
���� | 80 | b | 80 | d |
��ΰ | a | 85 | c | 260 |
��a=�� ����b=�� ����c=�� ����d=�� ����
��2����90�����ϣ���90�֣��ijɼ���Ϊ���㣬�������ʸߵ����� ����
��3������Ҫ��������ͬѧѡһλȥ�μ���ѧ����������Ը������ϵ����ݸ���ʦ��Щ���飿
���𰸡���1��80��80��90��60��2����ΰ��3����ΰ
��������
(1)����ƽ��������λ��������,����Ķ���ֱ����ɵ�;
(2)�����ṩ����,���Էֱ�������˵�������,���ɵó���;
(3)���Դ�����ƽ���ɼ��������ʵó���.
��1������10�γɼ��ֱ�Ϊ��80��70��90��80��70��90��70��80��90��80��
����С˳������Ϊ��70��70��70��80��80��80��80��90��90��90��
�����b=80��
����d=![]() ��[��80��80��2��4+��70��80��2��3+��90��80��2��3]=60��
��[��80��80��2��4+��70��80��2��3+��90��80��2��3]=60��
��ΰ��ƽ���ɼ�a=![]() =80���֣���
=80���֣���
90������3�Σ����ֵĴ�����࣬������c=90��
�ʴ�Ϊ��80��80��90��60��
��2����������������![]() ��100%=30%��
��100%=30%��
�����������![]() ��100%=50%��
��100%=50%��
����ΰ�������ʸߣ�
�ʴ�Ϊ����ΰ��
��3������������ΰ��ƽ���ɼ���ͬ������ΰ�������ʸ���������
������ѡ��ΰ�μӾ�����

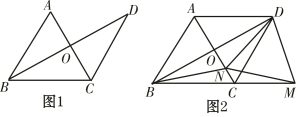
����Ŀ���ӱ߳�Ϊa�Ĵ�������ֽ������ȥһ���߳�Ϊb��С�����κ���ó��ĸ���ͬ�ĵ������Σ���ͼ1����Ȼ��ƴ��һ��ƽ���ı��Σ���ͼ2������ôͨ����������ͼ�ε���Ӱ���ֵ������������֤�����Ĺ�ʽ�ǣ� ��
A��a2��b2=(a��b)2 | B��(a+b)2="a+2ab+b" |
C��(a��b)2=a2��2ab+b2 | D��a2��b2=(a��b)(a+b) |