Question

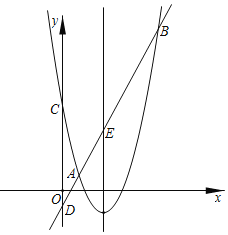
【题目】如图，抛物线y=ax2+bx+5(a≠0)交直线y=kx+n(k＞0)于A(1，1)，B两点，交y轴于点C，直线AB交y轴于点D．已知该抛物线的对称轴为直线x=．

(1)求a，b的值；

(2)记直线AB与抛物线的对称轴的交点为E，连接CE，CB．若△CEB的面积为，求k，n的值．

Answer 1

【答案】(1)a的值为1，b的值为–5；(2)k的值为2，n的值为–1．

【解析】

（1）根据抛物线y＝ax2＋bx＋5（a≠0）过A（1，1），对称轴为直线x＝，列出关于a、b的方程组，解方程组即可求出a，b的值；

（2）设点B（m，m25m＋5），过A作AG⊥y轴于G，过B作BF⊥x轴于F，延长GA交BF于H．由DG∥BF，得出=，求出DG＝m4，那么CD＝m．根据S△CEB＝S△CDBS△CDE，列出方程m2–m×=，求出m．再把A、B两点的坐标代入y＝kx＋n，即可求出k，n的值．

解：(1)由题意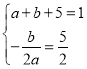，得，解得，

故所求a的值为1，b的值为–5；

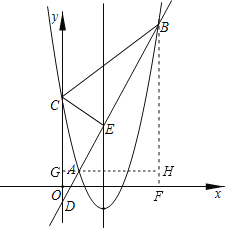
(2)由(1)可得y=x2–5x+5．可得C(0，5)．

如图，设点B(m，m2–5m+5)，

过A作AG⊥y轴于G，过B作BF⊥x轴于F，延长GA交BF于H．

∵DG∥BF，∴=，

即=，

∴DG=m–4，∴CD=m．

∵S△CEB=S△CDB–S△CDE，

∴m2–m×=，

解得m1=– (舍去)，m2=6．

把A(1，1)，B(6，11)代入y=kx+n，

得，解得．

故所求k的值为2，n的值为–1．