题目内容
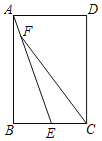
【题目】如图,在矩形ABCD中,点E是BC上一点,连接AE,点F是AE上一点,连接FC,若∠BAE=∠EFC,CF=CD,AB:BC=3:2,AF=4,则FC的长为_____.
【答案】6![]()
【解析】
根据矩形的性质得到AB=CD,过B作BG⊥AE于G,过C作CH⊥AE于H,根据全等三角形的性质得到AG=FH,BG=CH,求得AF=GH=4,根据全等三角形的性质得到GE=HE=2,BE=CE,设AB=CF=3x,BC=2x,根据勾股定理得到AE=![]() =
=![]() ,列方程即可得到结论.
,列方程即可得到结论.
解:∵四边形ABCD是矩形,
∴AB=CD,
∵CF=CD,
∴AB=CF,
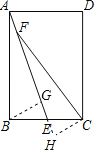
过B作BG⊥AE于G,过C作CH⊥AE于H,
∴∠AGB=∠FHC=90°,
在△ABG与△FCH中,
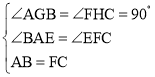 ,
,
∴△ABG≌△FCH(AAS),
∴AG=FH,BG=CH,
∴AF=GH=4,
在△EBG与△ECH中,
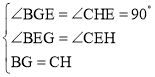 ,
,
∴△EBG≌△ECH(AAS),
∴GE=HE=2,BE=CE,
∵AB:BC=3:2,
∴设AB=CF=3x,BC=2x,
∴BE=CE=x,
∴AE=![]() =
=![]() ,
,
∵∠ABC=90°,BG⊥AE,
∴△BEG∽AEB,
∴BE2=EGAE,
∴AE=![]() ,
,
∴![]() ,
,
∴x=2![]() ,x=0(不合题意舍去),
,x=0(不合题意舍去),
∴CF=3x=6![]() ,
,
故答案为6![]() .
.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目