题目内容
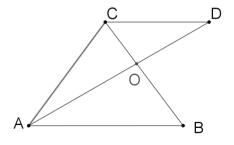
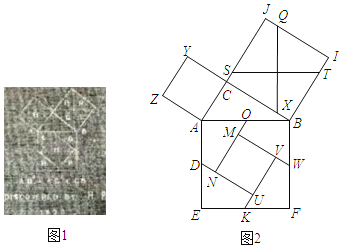
【题目】勾股定理有着悠久的历史，它曾引起很多人的兴趣．英国佩里加（H．Perigal，1801﹣1898）用“水车翼轮法”（图1）证明了勾股定理．该证法是用线段QX，ST，将正方形BIJC分割成四个全等的四边形，再将这四个四边形和正方形ACYZ拼成大正方形AEFB（图2）．若AD＝
，tan∠AON＝
，则正方形MNUV的周长为（ ）
A. 
B. 18C. 16D. 
【答案】C
【解析】
延长QN交AE于H．解直角三角形求出OH，HN，OM即可解决问题．
解：延长QN交AE于H．
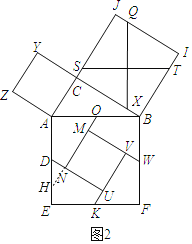
由题意AO＝AD＝DE＝
，AE＝
，
在Rt△AOH中，∵tan∠AOH＝
，
∴AH＝
，
∴OH＝
，DH＝AH＝AD＝
，
∵△NHD∽△HAO，
∴
，
∴DN＝1，HN＝
，
∴ON＝OH﹣HN＝5，
∵OM＝DN＝1，
∴MN＝5﹣1＝4，
∴正方形MNUV的周长为16，
故选：C．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
