Question

【题目】在平面直角坐标系中，已知二次函数的图象与x轴交于点，与y轴交于点B，将其图象在点A，B之间的部分（含A，B两点）记为F．

（1）求点B的坐标及该函数的表达式；

（2）若二次函数的图象与F只有一个公共点，结合函数图象，求a的取值范围．

Answer 1

【答案】（1）点B的坐标为． ． （2）或．

【解析】

（1）令x=0可求出y的值，从而得到点B的坐标；把点A坐标代入求出m的值即可得到结论；

（2）画出函数图象，再利用图象确定a的取值范围即可.

（1）∵的图象与y轴交于点B，

∴点B的坐标为．

∵的图象与x轴交于点，

∴将代入可得．

∴．

∴该函数的表达式为．

（2）∵将二次函数的图象在点A，B之间的部分（含A，B两点）记为F，

∴F的端点为A，B，并经过抛物线的顶点C（其中C点坐标为）．

∴可画F如图1所示．

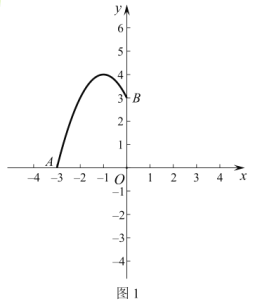
∵二次函数的图象的对称轴为，且与F只有一个公共点，

∴可分别把A，B，C的坐标代入解析式中．

∴可得三个a值分别为，3，5．

画示意图如图2所示．

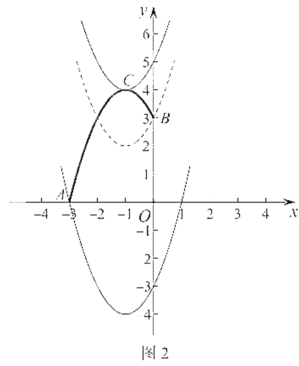
∴结合函数图象可知：

二次函数的图象与F只有一个公共点时，a的取值范围是或．