题目内容
【题目】已知⊙O及⊙O上一点P,过点P作⊙O的切线.
小明设计了如下尺规作法:
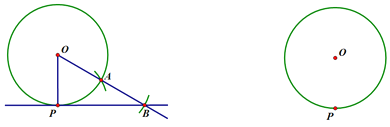
①连接OP,以点P为圆心,OP长为半径画弧交⊙O于点A;
②连接OA,延长OA到B,使AB=OA,作直线PB.则直线即为所求作.
(1)请证明小明作法的正确性;
(2)请你自己再设计一种尺规作图方法(保留痕迹,不要证明).
【答案】(1)见解析;(2)见解析;
【解析】
(1)连接![]() ,证出
,证出![]() 即可;
即可;
(2)先作一条射线OP,然后在OP外取一点A, 再以点A为圆心,AP为半径作圆,与射线OP交于另一点B,连接并延长BA与⊙A交于点C,连接PC即可.
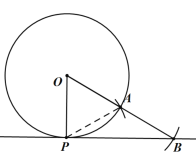
证明:(1)连接![]() ,由题意可知:
,由题意可知:![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]()
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,
即:![]() 为⊙O的切线;
为⊙O的切线;
(2)解:作法:
①作射线OP;
②在射线OP外任取一点A, 以点A为圆心,AP为半径作⊙A,与射线OP交于另一点B;
③连接并延长BA与⊙A交于点C;
④作直线PC;
则直线PC即为所求.如下图所示:
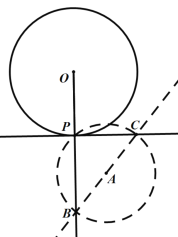
证明:∵BC是⊙A的直径,
∴∠BPC=90° (圆周角定理 ) ,
即OP⊥PC,
又∵OP是⊙O的半径,
∴PC是⊙O的切线(切线的判定) .

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案【题目】小颖“综合与实践”小组学习了三角函数后,开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,如表是不完整测量数据.
课题 | 测量旗杆的高度 | |||
成员 | 组长:小颖,组员:小明,小刚,小英 | |||
测量工具 | 测量角度的仪器,皮尺等 | |||
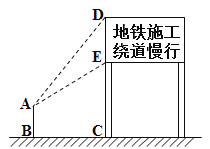
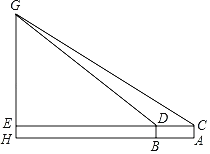
测量示意图 |
| 说明: 线段GH表示学校旗杆,测量角度的仪器的高度AC=BD=1.62m,测点A,B与H在同一水平直线上,A,B之间的距离可以直接测得,且点G,H,A,B,C,D都在同一竖直平面内,点C,D,E在同一条直线上,点E在GH上. | ||
测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 |
∠GCE的度数 | 30.6° | 31.4° | 31° | |
∠GDE的度数 | 36.8° | 37.2° | 37° | |
A,B之间的距离 | 10.1m | 10.5m | m | |
… | … | |||
(1)任务一:完成表格中两次测点A,B之间的距离的平均值.
(2)任务二:根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆GH的高度.(精确到0.1m)(参考数据:sin31°≈0.51,cos31°≈0.86,tan31°≈0.60,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)