题目内容
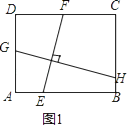
【题目】如图1，在平面直角坐标系中，矩形 ABCO，B点坐标为（4,3），抛物线y=
经过矩形ABCO的顶点 B 、C ，D为BC的中点，直线 AD y轴交 E点，与抛物线 
交于第四象限的 F点．
（1）求该抛物线解析式与F点坐标；
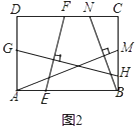
（2）如图2，动点P从点C出发，沿线段 CB以每秒1个单位长度的速度向终点B运动；同时，动点M从 A出发，沿线 AE以每秒 
个单位长度的速度向终点E运动．过点P作PH ⊥OA，垂足为H ，连接 MP ，MH ．设点 P 的运动时间 t秒．
①问EP+ PH+ HF是否有最小值？如果有,求出t的值；如果没有，请说明理由．
②若△PMH是等腰三角形，请直接写出此时t的值．
【答案】
（1）解：∵矩形ABCO中点B的坐标为（4，3），
∴点C（0，3），
∵抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C，
∴
,
解得：
，
∴抛物线的解析式为：y=x2+2x+3 ①，
设直线AD的解析式为y=kx+m，
∵A（4，0），D（2，3），
∴
，
解得：
，
∴直线AD的解析式为y=
x+6 ②，
联立①②两式，且点F在第四象限，
∴点F（6，-3）
（2）解：①如图（1）：
∵E（0，6），
∴CE=CO，
连接CF交x轴于H'，过点H'作H'P'⊥BC与点P'，
当P运动到P'，当H运动到H'时，EP+ PH+ HF的值最小.
设直线CF的解析式为y=kx+b，
∵C（0,3），F（6，-3），
∴
，
解得：
，
∴y=-x+3，
∴H'（3，0）
∴CP=3，
∴t=3.
②如图1：过点M作MN⊥OA于点N，
∵
AMNAEO，
∴
，
即：
，
∴AN=t，MN=
t，
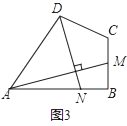
（I）如图3，当PM=HM时，点M在PH的垂直平分线上，
∴MN=
PH，
∴MN=t=，
∴t=1；
（II）如图1，当HM=HP时，MH=3，MN=t，
HN=OA-AN-OH=4-2t，
在RtHMN中，MN2+HN2=MH2，
∴（t）2+（4-2t）2=32，
解得：t1=2（舍去），t2=
；
（III）如图2，图4，当PH=PM时，
∵PM=3，MT=|3-t|，PT=BC-CP-BT=|4-2t|，
∴在RtPMT中，MT2+PT2=PM2，
即：（3-t）2+（4-2t）2=32，
解得：t1=
，t2=
；
综上，t=1，t=，t=，t=.
【解析】（1）由矩形的性质可求出点C的坐标，用待定系数法求得抛物线的解析式，再根据点A和点D的坐标，用待定系数法求得一次函数的解析式，再联立二次函数和一次函数的解析式即可求出点F的坐标；（2）①根据题意作出辅助线，当P运动到P'，当H运动到H'时，EP+ PH+ HF的值最小；②根据题意作出辅助线，再分情况讨论，求出t的值即可.
