题目内容
【题目】【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
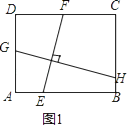
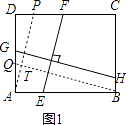
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() =
= ![]() ;
;
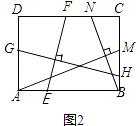
(2)【结论应用】如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 ![]() =
= ![]() ,则
,则 ![]() 的值为;
的值为;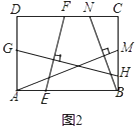
(3)【联系拓展】如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 ![]() 的值.
的值.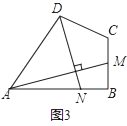
【答案】
(1)解:过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,
∵四边形ABCD是矩形,∴AB∥DC,AD∥BC.
∴四边形AEFP、四边形BHGQ都是平行四边形,
∴AP=EF,GH=BQ.
又∵GH⊥EF,∴AP⊥BQ,
∴∠QAT+∠AQT=90°.
∵四边形ABCD是矩形,∴∠DAB=∠D=90°,
∴∠DAP+∠DPA=90°,
∴∠AQT=∠DPA.
∴△PDA∽△QAB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ;
;
(2)![]()
(3)解:过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,
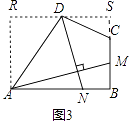
则四边形ABSR是平行四边形.
∵∠ABC=90°,∴ABSR是矩形,
∴∠R=∠S=90°,RS=AB=10,AR=BS.
∵AM⊥DN,
∴由(1)中的结论可得 ![]() =
= ![]() .
.
设SC=x,DS=y,则AR=BS=5+x,RD=10﹣y,
∴在Rt△CSD中,x2+y2=25①,
在Rt△ARD中,(5+x)2+(10﹣y)2=100②,
由②﹣①得x=2y﹣5③,
解方程组 ![]() ,得
,得
![]() (舍去),或
(舍去),或 ![]() ,
,
∴AR=5+x=8,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【解析】(2)解:如图2,
∵EF⊥GH,AM⊥BN,
∴由(1)中的结论可得 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() .
.
所以答案是 ![]() ;
;
【考点精析】本题主要考查了勾股定理的概念和平行四边形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.

【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | 27 |
C | 10000<x≤15000 | m |
D | 15000<x≤20000 | 33 |
E | x>20000 | 30 |
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有 户,表中m= ;
(2)请说明本次调查数据的中位数落在哪一组?
(3)在扇形统计图中,D组所在扇形的圆心角为多少度?
(4)这个社区有2500户家庭,请你估计年文化教育消费在10000元以上的家庭有多少户?

【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?