题目内容
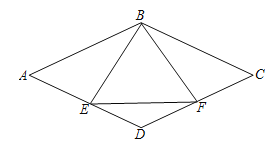
【题目】如图是一个汉字“互”字，其中，AB∥CD，∠1=∠2，∠MGH=∠MEF.
求证：∠MEF=∠GHN.
证明：∵ AB∥CD（已知）
∴∠1=∠3（ ）
又∵∠1=∠2（已知）
∴∠2=∠3（ ）
∴ME∥HN （ ）
∴∠MGH=∠ ( )( )
又∵∠MGH=∠MEF (已知)
∴∠MEF=∠GHN（ ）
【答案】两直线平行，内错角相等; 等量代换; 同位角相等，两直线平行; GHN; 两直线平行，内错角相等; 等量代换.
【解析】
由AB∥CD．可得∠1=∠3，等量代换易得∠2=∠3，由平行线的判定定理可得ME∥HN，易得∠MGH=∠GHN，等量代换易得结论．
证明：∵ AB∥CD（已知）
∴∠1=∠3（两直线平行，内错角相等）
又∵∠1=∠2（已知）
∴∠2=∠3（等量代换）
∴ME∥HN （同位角相等，两直线平行）
∴∠MGH=∠(GHN)(两直线平行，内错角相等)
又∵∠MGH=∠MEF (已知)
∴∠MEF=∠GHN（等量代换）
练习册系列答案
名校课堂系列答案
相关题目
