题目内容
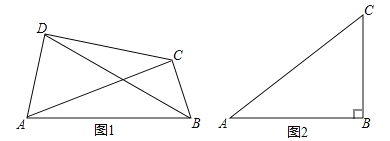
【题目】如图1,在四边形ABCD中,如果对角线AC和BD相交并且相等,那么我们把这样的四边形称为等角线四边形.
(1)①在“平行四边形、矩形、菱形”中, 一定是等角线四边形(填写图形名称);
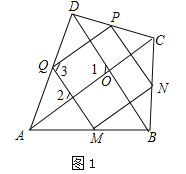
②若M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD.DA的中点,当对角线AC、BD还要满足 时,四边形MNPQ是正方形.
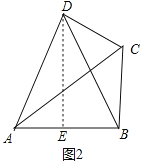
(2)如图2,已知△ABC中,∠ABC=90°,AB=4,BC=3,D为平面内一点.
①若四边形ABCD是等角线四边形,且AD=BD,则四边形ABCD的面积是 ;
②设点E是以C为圆心,1为半径的圆上的动点,若四边形ABED是等角线四边形,写出四边形ABED面积的最大值,并说明理由.
【答案】(1)①矩形;②AC⊥BD;(2)①3+2![]() ;②18.
;②18.
【解析】试题(1)①只有矩形的对角线相等,所以矩形是等角线四边形;
②当AC⊥BD时,四边形MNPQ是正方形,首先证明四边形MNPQ是菱形,再证明有一个角是直角即可;
(2)①如图2中,作DE⊥AB于E.根据S四边形ABCD=S△ADE+S梯形DEBC计算,求出相关线段即可;
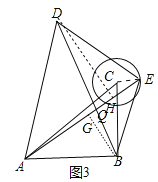
②如图3中,设AE与BD相交于点Q,连接CE,只要证明当AC⊥BD且A、C、E共线时,四边形ABED的面积最大即可.
试题解析:(1)①在“平行四边形、矩形、菱形”中,
∵矩形的对角线相等,∴矩形一定是等角线四边形,
故答案为:矩形.
②当AC⊥BD时,四边形MNPQ是正方形.
理由:如图1中,∵M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点,∴PQ=MN=![]() AC,PN=QM=
AC,PN=QM=![]() BD,PQ∥AC,MQ∥BD,
BD,PQ∥AC,MQ∥BD,
∵AC=BD,∴MN=NP=PQ=QM,∴四边形MNPQ是菱形,
∵∠1=∠2,∠2=∠3,∠1=90°,∴∠3=90°,
∴四边形NMPQ是正方形.
故答案为:AC⊥BD.
(2)①如图2中,作DE⊥AB于E.
在Rt△ABC中,∵∠ABC=90°,AB=4,BC=3,∴AC=![]() =5,
=5,
∵AD=BD,DE⊥AB,∴AE=BD=2,
∵四边形ABCD是等角线四边形,∴BD=AC=AD=5,在Rt△BDE中,DE=![]() =
=![]() ,∴S四边形ABCD=S△ADE+S梯形DEBC
,∴S四边形ABCD=S△ADE+S梯形DEBC
=![]() AEDE+
AEDE+![]() (DE+BC)BE=
(DE+BC)BE=![]() ×2×
×2×![]() +
+![]() (
(![]() +3)×2=3+2
+3)×2=3+2![]() ,
,
故答案为:3+2![]() ;
;
②如图3中,设AE与BD相交于点Q,连接CE,作DH⊥AE于H,BG⊥AE于G.则DH≤DQ,BG≤BQ,∵四边形ABED是等角线四边形,∴AE=BD,
∵S四边形ABED=S△ABE+S△ADE=![]() AEDH+
AEDH+![]() AEBG=
AEBG=![]() AE(GB+DH)≤
AE(GB+DH)≤![]() AE(BQ+QD),即S四边形ABED≤
AE(BQ+QD),即S四边形ABED≤![]() AEBD,
AEBD,
∴当G、H重合时,即BD⊥AE时,等号成立,
∵AE=BD,∴S四边形ABED≤![]() AE2,即线段AE最大时,四边形ABED的面积最大,
AE2,即线段AE最大时,四边形ABED的面积最大,
∵AE≤AC+CE,∴AE≤5+1,∴AE≤6,∴AE的最大值为6,
∴当A、C、E共线时,取等号,∴四边形ABED的面积的最大值为![]() ×62=18.
×62=18.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案【题目】下表是某网约车公司的专车计价规则.
计费项目 | 起租价 | 里程费 | 时长费 | 远途费 |
单价 | 15元 | 2.5元/公里 | 1.5元/分 | 1元/公里 |
注:车费由起租价、里程费、时长费、远途费四部分构成,其中起租价15元含10分钟时长费和5公里里程费,远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收1元.
(1)若小李乘坐专车,行车里程为20公里,行车时间为30分,则需付车费_______元.
(2)若小李乘坐专车,行车里程为![]() 公里,平均时速为
公里,平均时速为![]() ,则小李应付车费多少元? (用含
,则小李应付车费多少元? (用含![]() 的代数式表示)
的代数式表示)
(3)小李与小王各自乘坐专车,行车车费之和为76元,里程之和为15公里(其中小王的行车里程不超过5公里).如果行驶时间均为 20分钟,那么这两辆专车此次的行驶路程各为多少公里?