题目内容
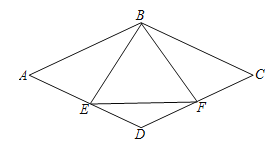
【题目】如图,点E、F分别为菱形ABCD边AD、CD的中点.
(1)求证:BE=BF;
(2)当△BEF为等边三角形时,求证:∠D=2∠A.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)根据菱形的性质得到AB=CB,AD=CD,∠A=∠C,再根据中点的定义得到AE=CF,根据SAS可证△BAE≌△BCF,根据全等三角形的性质得到BE=BF即可;
(2)作辅助线,先根据线段垂直平分线的逆定理证明BD是EF的垂直平分线,由等边三角形三线合一得:EG=FG,∠EBG=![]() ∠EBF=30°,设EG=x,则BE=2x,BG=
∠EBF=30°,设EG=x,则BE=2x,BG=![]() x,根据中位线定理得:AO=2EG=2x,OB=
x,根据中位线定理得:AO=2EG=2x,OB=![]() x,证明△BHO∽△BEG,列比例式可得OH=
x,证明△BHO∽△BEG,列比例式可得OH= ![]() ,BH=
,BH=![]() x,再求AH=
x,再求AH=![]() x,则AH=BH,可得∠DAB=60°,∠ADC=120°,从而得出结论.
x,则AH=BH,可得∠DAB=60°,∠ADC=120°,从而得出结论.
试题解析:证明:(1)∵四边形ABCD是菱形,∴∠A=∠C,AB=BC=AD=CD.∵点E、F分别为菱形ABCD边AD、CD的中点,∴AE=![]() AD,CF=
AD,CF=![]() CD,∴AE=CF,∴△ABE≌△CBF(SAS),∴BE=BF;
CD,∴AE=CF,∴△ABE≌△CBF(SAS),∴BE=BF;
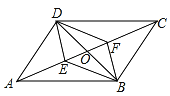
(2)如图,连接AC、BD交于点O,设BD与EF交于G,AC与BE交于H,则AC⊥BD.∵BE=BF,ED=DF,∴BD是EF的垂直平分线,∴EG=FG,∠EBG=![]() ∠EBF=30°,Rt△BEG中,设EG=x,则BE=2x,BG=
∠EBF=30°,Rt△BEG中,设EG=x,则BE=2x,BG=![]() x.∵EG∥AO,E为AD的中点,∴G是OD的中点,∴AO=2EG=2x,OB=
x.∵EG∥AO,E为AD的中点,∴G是OD的中点,∴AO=2EG=2x,OB=![]() x.∵OH∥GE,∴△BHO∽△BEG,∴
x.∵OH∥GE,∴△BHO∽△BEG,∴![]() ,∴
,∴![]() =
=![]() =
=![]() ,∴OH=
,∴OH= ![]() ,BH=
,BH=![]() x,∴AH=AO﹣OH=2x﹣
x,∴AH=AO﹣OH=2x﹣![]() x=
x=![]() x,∴AH=BH,∴∠HAB=∠ABH.∵∠BHC=∠HAB+∠ABH=60°,∴∠HAB=30°,∴∠DAB=60°,∴∠ADC=120°,∴∠ADC=2∠DAB,即∠D=2∠A.
x,∴AH=BH,∴∠HAB=∠ABH.∵∠BHC=∠HAB+∠ABH=60°,∴∠HAB=30°,∴∠DAB=60°,∴∠ADC=120°,∴∠ADC=2∠DAB,即∠D=2∠A.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案