题目内容
【题目】如图1，已知抛物线
与y轴交于点A（0，﹣4），与x轴相交于B（﹣2，0）、C（4，0）两点，O为坐标原点．
（1）求抛物线的解析式；
（2）设点E在x轴上，∠OEA+∠OAB=∠ACB，求BE的长；
（3）如图2，将抛物线y=ax2+bx+c向右平移n（n＞0）个单位得到的新抛物线与x轴交于M、N（M在N左侧），P为x轴下方的新抛物线上任意一点，连PM、PN，过P作PQ⊥MN于Q，
是否为定值？请说明理由．
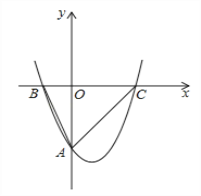
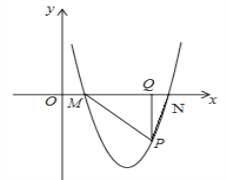
图1 图2
【答案】（1）y=
x2-x-4；（2）14或10；（3）是定值，理由见解析.
【解析】（1）由题意设抛物线解析式为y=a（x+2）（x-4），把（0，-4）代入求出a即可．
（2）由tan∠ACB=
=1，tan∠OAB=
=，可得tan∠OEA=
，即
=，从而根据正切函数的定义求出OE的值，进而可求BE的值；
（3）设平移后的解析式为y=(x+2-n)(x-4-n) ，点P的坐标为P(t,(t+2-n)(t-4-n))，
表示出PQ、 MQ、NQ后，代入
+
化简即可.
设（1）y=a(x+2)(x-4)，将（0，-4）代入，得
-8a=-4a,
∴a=，
∴y=(x+2)(x-4)，即y=x2-x-4；
(2). Rt△AOC中，tan∠ACB=
=1；
Rt△AOC中，tan∠OAB=
=，
∵∠OEA=∠ACB-∠OAB，
∴tan∠OEA=
=，即
=，
∵OA=4，
∴OE=12，
∴BE=12+2=14或BE=12-2=10，
答：BE的长为14或10；
（3）平移后：y=(x+2-n)(x-4-n) ，
∴ M(-2+n,0)， N(4+n,0)，
设P(t,(t+2-n)(t-4-n))，
则PQ=-(t+2-n)(t-4-n)，
MQ=t-(-2-n)=t+2-n， NQ=4+n-t，
∴
+
=
+
=- (t-4-n)+(t+2-n)=3为定值.
