Question

【题目】阅读下列材料：若要比较与的大小．我们可以利用不等式的性质来说明：

例加：若，则；若，则；若，则．

像上述比较两个代数式大小的方法叫做作差法．

如：某同学需要比较与的大小，做法为，则．试解答下列问题：

（1） 比较大小：

（2） 若，试用作差法比较与的大小关系，并说明理由；

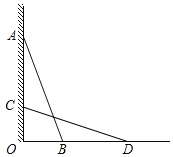
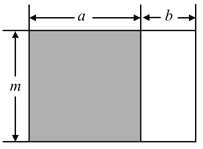
（3）若某三角形的底和高均为，某长方形的长宽为和，试比较这两个图形的面积大小，并说明理由；(其中)

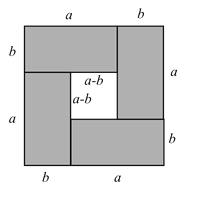
（4）“无字证明”是数学中非常重要的一种解决方法．课本在证明时，运用了如图中的图形面积来证明．某同学提出运用图形的几何意义的方法不仅可以解决等式的证明，也可以解决不等式的相关证明．如对（2）问中的的大小关系的证明，当时，若使用图形的几何意义可以更为直观解决，请你画出符合题意的图形，并简要说明．

Answer 1

【答案】（1）>；（2），理由见解析；（3）三角形面积大于长方形面积，理由见解析；（4）图见解析，说明见解析

【解析】

（1）根据作差法，计算的结果，与0作比较即可；

（2）求出即可得出结果；

（3）首先分别求出三角形和长方形的面积，然后利用作差法进行比较；

（4）作出以a+b为边长的正方形和以a，b为长宽的长方形的组合图形即可.

解：（1）∵，

∴，

故答案为：>；

（2），

理由：∵，

∴；

（3）三角形面积大于长方形面积，

理由：，，

∵，，

∴，即；

如图所示：表示大正方形的面积，表示四个小矩形的面积，表示中间空白处以为边长的正方形的面积，所以．