Question

【题目】如图，B、C、D在同一直线上，△ABC和△DCE都是等边三角形，且在直线BD的同侧，BE交AD于F，BE交AC于M，AD交CE于N.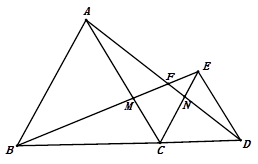

（1）求证：AD=BE；
（2）求证：△ABF∽△ADB。

Answer 1

【答案】
（1）

证明： ∵△ABC和△DCE都是等边三角形

∴BC=AC，CE=CD,ACB=EDC=60°

∴ACB+ACE=EDC+ACE，即：BCE=ACD

在△BCE与△ACD 中，

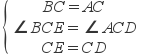
∴△BCE≌△ACD (SAS)

∴ AD=BE

（2）

证明：由（1）知：△BCE≌△ACD

∴ ∠CBE=∠CAD

又∵∠BMC=∠AMF

∴ ∠AFB=∠ACB=60°=∠ABC

又∵∠ABM=∠FBA

∴ △ABF∽△ADB

【解析】本题考查的是等边三角形的判定与性质、全等三角形的判定与性质及相似三角形的判定与性质，熟知全等三角形、相似三角形的判定定理，准确找出合适的全等三角形，再充分利用性质是解答此题的关键.