题目内容
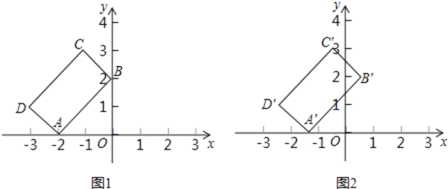
【题目】在平面直角坐标系xOy中,矩形ABCD的位置如图1所示,点A的坐标为(-2,0),点B的坐标为(0,2),点D的坐标为(-3,1).矩形ABCD以每秒1个单位长度的速度沿x轴正方向运动,设运动时间为x(0≤x≤3)秒,第一象限内的图形面积为y,则下列图象中表示y与x的函数关系的图象大致是
A. 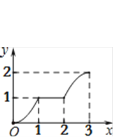 B.
B. 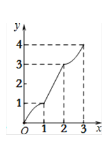 C.
C. 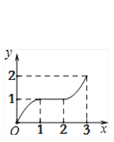 D.
D. 
【答案】D
【解析】根据点A、B、D的坐标求出OA=OB=2,△AOB是等腰直角三角形,AD= ![]() ,AB=
,AB= ![]() ,再根据矩形的性质得出AD=BC=
,再根据矩形的性质得出AD=BC=![]() ,AB=CD=
,AB=CD=![]() ,∠DAB=∠ABC=∠C=∠D=90°,当矩形从第二象限移至第一象限时应分三种情况进行讨论:①当0≤x≤1时,矩形ABCD落在第一象限内的图形是三角形FB′G,利用三角形的面积公式表示出y与x的函数关系式,②当1<x≤2时,矩形ABCD落在第一象限内的图形是梯形FB′C′G,利用梯形的面积公式表示出y与x的函数关系式,③当2<x≤3时,矩形ABCD落在第一象限内的图形是五边形FA′B′C′G,利用矩形的面积减去三角形的面积,列式整理得到y与x的函数关系式,从而判断出函数图象.
,∠DAB=∠ABC=∠C=∠D=90°,当矩形从第二象限移至第一象限时应分三种情况进行讨论:①当0≤x≤1时,矩形ABCD落在第一象限内的图形是三角形FB′G,利用三角形的面积公式表示出y与x的函数关系式,②当1<x≤2时,矩形ABCD落在第一象限内的图形是梯形FB′C′G,利用梯形的面积公式表示出y与x的函数关系式,③当2<x≤3时,矩形ABCD落在第一象限内的图形是五边形FA′B′C′G,利用矩形的面积减去三角形的面积,列式整理得到y与x的函数关系式,从而判断出函数图象.
如图1,∵点A的坐标为(﹣2,0),点B的坐标为(0,2),点D的坐标为(﹣3,1),
∴OA=OB=2,△AOB是等腰直角三角形,AD=![]() =
=![]() ,
,
∴AB=2![]() ,
,
∵四边形ABCD是矩形,
∴AD=BC=![]() ,AB=CD=2
,AB=CD=2![]() ,∠DAB=∠ABC=∠C=∠D=90°.
,∠DAB=∠ABC=∠C=∠D=90°.
分三种情况:




当0≤x≤1时如图2所示,矩形ABCD落在第一象限内的图形是等腰直角△FB′G,
∴FG=2x,
∴y=![]() 2x
2x![]() x =
x =![]()
当1<x≤2时,矩形ABCD落在第一象限内的图形是梯形FB′CG,如图3.
∵OA′=2﹣x,△A′OF是等腰直角三角形,
∴A′F= OA′= (2﹣x),
∴FB′=A′B′﹣A′F=![]() ﹣
﹣![]() =
= ![]() ,
,
C′G=![]() =
= ![]()
∴y= ![]() (C′G+B′F)B′C′=
(C′G+B′F)B′C′= ![]() (
( ![]() +
+ ![]() )×
)×![]() =2x﹣1;
=2x﹣1;
当2<x≤3时,矩形ABCD落在第一象限内的图形是五边形FA′B′CG,如图4.
∵FG=2(3-x)=6-2x,△D′FG是等腰直角三角形,
∴△D′FG的面积是![]() (6-2x)(3-x)=
(6-2x)(3-x)=![]() ,
,
∴y=4-(![]() )=
)=![]() ﹣x2+6x﹣5.
﹣x2+6x﹣5.
故D选项正确.