题目内容
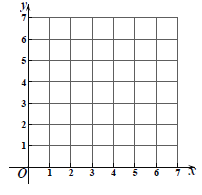
【题目】如图,在平面直角坐标系中,直线y=﹣5x+5与x轴、y轴分别交于A,C两点,抛物线y=x2+bx+c经过A,C两点,与x轴交于另一点B.
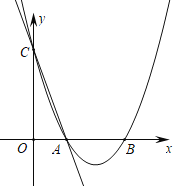
(1)求抛物线解析式及B点坐标;
(2)x2+bx+c≥﹣5x+5的解集 .
(3)若点M在第一象限内抛物线上一动点,连接MA、MB,当点M运动到某一位置时,△ABM面积为△ABC的面积的![]() 倍,求此时点M的坐标.
倍,求此时点M的坐标.
【答案】(1)点B(5,0);(2)x≤0或x≥1;(3)点M(3+2![]() ,4)或(3﹣2
,4)或(3﹣2![]() ,4).
,4).
【解析】
(1)根据一次函数解析式求出点A、C的坐标,将点A、C的坐标代入抛物线表达式,即可求出抛物线解析式,易得B点坐标;
(2)x2+bx+c≥5x+5表示抛物线在直线的上方,从图象上分析函数交点情况,即可求解;
(3)由△ABM面积为△ABC的面积的![]() 倍得:
倍得:![]() ×AB×|yM|=
×AB×|yM|=![]() ×AB×CO×
×AB×CO×![]() ,即可求解.
,即可求解.
(1)直线y=﹣5x+5与x轴、y轴分别交于A,C两点,
当x=0时,y=5,当y=0时,x=1,
则点A、C的坐标分别为:(1,0)、(0,5),
将点A、C的坐标代入抛物线表达式得:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:y=x2﹣6x+5,
令y=0,解得:x=1或5,
故点B(5,0);
(2)x2+bx+c≥﹣5x+5的解集从图象看表示的是抛物线在直线的上方对应的x的取值范围,
∴解集是:x≤0或x≥1,
故答案为:x≤0或x≥1;
(3)设点M(x,x2﹣6x+5),
由△ABM面积为△ABC的面积的![]() 倍得:
倍得:![]() ×AB×|yM|=
×AB×|yM|=![]() ×AB×CO×
×AB×CO×![]() ,
,
即:|x2﹣6x+5|=5×![]() ,
,
解得:x=3![]() (不合题意的值已舍去),
(不合题意的值已舍去),
故点M(3+2![]() ,4)或(3﹣2
,4)或(3﹣2![]() ,4).
,4).

练习册系列答案
相关题目