ЬтФПФкШн
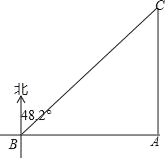
ЁОЬтФПЁПШчЭМЃЌдквЛДЮКЃОЏбнЯАжаЃЌAЁЂBСНЕиЗжБ№ЭЌЪБХЩГіМзЁЂввСНПьЭЇгЊОШвЛЛѕТжCЃЌвбжЊBЕиЮЛгкAЕие§ЮїЗНЯђЯрОр84КЃРяЮЛжУЃЌЛѕТжCЮЛгкAЕие§ББЗНЯђЃЌЮЛгкBЕиББЦЋЖЋ48.2ЁуЗНЯђЃЈЫљгаЪ§ОнОЋШЗЕНИіЮЛЃЌsin48.2ЁуЁж0.7ЃЌcos48.2ЁуЁж0.6ЃЌtan48.2ЁуЁж1.05ЃЉ
ЃЈ1ЃЉЧѓAЁЂBСНЕиЗжБ№гыЛѕТжCЕФОрРыЃЛ
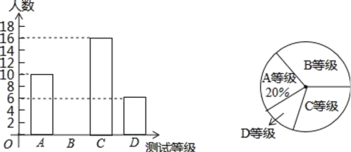
ЃЈ2ЃЉШєввПьЭЇУПаЁЪББШМзПьЭЇЖрааЪЛ20КЃРяЃЌЧвЫќУЧЭЌЪБДяЕНЛѕТжCЮЛжУЃЌЧѓМзЁЂввПьЭЇЕФЫйЖШЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЁЂBСНЕиЗжБ№гыЛѕТжCЕФОрРыЮЊ80КЃРяЁЂ120КЃРяЃЛЃЈ2ЃЉМзЁЂввСНПьЭЇЕФЫйЖШЗжБ№ЮЊ40КЃРя/ЪБЁЂ60КЃРя/ЪБЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЕУГіИїНЧЕФЖШЪ§ЃЌНјЖјЕУГіBCЕФГЄЃЌМДПЩЕУГіACЕФГЄЃЎ
ЃЈ2ЃЉЩшМзПьЭЇЕФЫйЖШЮЊxКЃРя/ЪБЃЌИљОнЬтвтСаГіЗжЪНЗНГЬНтД№МДПЩЃЎ
НтЃКЃЈ1ЃЉвРЬтЃЌдкRtЁїABCжаЃЌЁЯC=48.2Ёу
Ёрsin48.2Ёу=![]() ЃЌtan48.2Ёу=
ЃЌtan48.2Ёу=![]()
ЁрBC![]() ЃЌAC
ЃЌAC![]()
МДAЁЂBСНЕиЗжБ№гыЛѕТжCЕФОрРыЮЊ80КЃРяЁЂ120КЃРяЃЎ
ЃЈ2ЃЉЩшМзПьЭЇЕФЫйЖШЮЊxКЃРя/ЪБЃЌдђввПьЭЇЕФЫйЖШЮЊЃЈx+20ЃЉКЃРя/ЪБЃЌ
Ёр![]()
НтЕУx=40
ОМьбщx=40ЪЧдЗНГЬЕФНтЃЌЗћКЯЬтвтЃЌ
Д№ЃКМзЁЂввСНПьЭЇЕФЫйЖШЗжБ№ЮЊ40КЃРя/ЪБЁЂ60КЃРя/ЪБЃЎ