题目内容
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
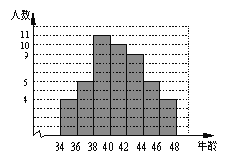
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
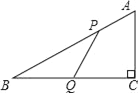
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
【答案】(1)△ABC是“等高底”三角形;(2)![]() ;(3)CD的值为
;(3)CD的值为![]() ,2
,2![]() ,2.
,2.
【解析】
(1)过A作AD⊥BC于D,则△ADC是直角三角形,∠ADC=90°,根据30°所对的直角边等于斜边的一半可得:![]() 根据“等高底”三角形的概念即可判断.
根据“等高底”三角形的概念即可判断.
(2)点B是![]() 的重心,得到
的重心,得到![]() 设
设![]() 则
则![]()
根据勾股定理可得![]() 即可求出它们的比值.
即可求出它们的比值.
(3)分两种情况进行讨论:①当![]() 时和②当
时和②当![]() 时.
时.
(1)△ABC是“等高底”三角形;
理由:如图1,过A作AD⊥BC于D,则△ADC是直角三角形,∠ADC=90°,

∵∠ACB=30°,AC=6,
∴![]()
∴AD=BC=3,
即△ABC是“等高底”三角形;
(2)如图2,∵△ABC是“等高底”三角形,BC是“等底”,

∴![]()
∵△ABC关于BC所在直线的对称图形是![]() ,
,
∴∠ADC=90°,
∵点B是![]() 的重心,
的重心,
∴![]()
设![]() 则
则![]()
由勾股定理得![]()
∴![]()
(3)①当![]() 时,
时,
Ⅰ.如图3,作AE⊥BC于E,DF⊥AC于F,
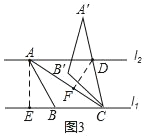
∵“等高底”△ABC的“等底”为BC,l1∥l2,l1与l2之间的距离为2,![]() .
.
∴![]()
∴BE=2,即EC=4,
∴![]()
∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,
∴∠DCF=45°,
设![]()
∵l1∥l2,
∴![]()
∴![]() 即
即![]()
∴![]()
∴![]()
Ⅱ.如图4,此时△ABC等腰直角三角形,

∵△ABC绕点C按顺时针方向旋转45°得到![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]()
②当![]() 时,
时,
Ⅰ.如图5,此时△ABC是等腰直角三角形,
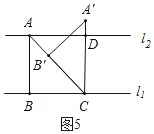
∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,
∴![]()
∴![]()
Ⅱ.如图6,作![]() 于E,则
于E,则![]()
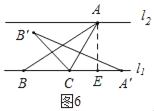
∴![]()
∴![]()
∴△ABC绕点C按顺时针方向旋转45°,得到![]() 时,点A'在直线l1上,
时,点A'在直线l1上,
∴![]() ∥l2,即直线
∥l2,即直线![]() 与l2无交点,
与l2无交点,
综上所述,CD的值为![]()