题目内容
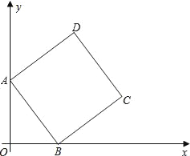
【题目】如图,在平面直角坐标系中,四边形ABCD是边长为5的正方形,顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA,OB的长满足|OA﹣4|+(OB﹣3)2=0.
(1)求OA,OB的长;
(2)求点D的坐标;
(3)在y轴上是否存在点P,使△PAB是以AB为腰的等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)OA=4,OB=3.(2)点D坐标为(4,7).(3)当PA=AB=5时,P(0,9)或(0,﹣1),当PB=BA时,P(0,﹣4).
【解析】
(1)利用非负数的性质即可解决问题.
(2)如图2中,作DE⊥y轴于E.证明△AOB≌△DEA(AAS),推出DE=OA=4,AE=OB=3,即可解决问题.
(3)分两种情形分别求解即可解决问题.
解:(1)∵|OA﹣4|+(OB﹣3)2=0,
又∵|OA﹣4|≥0,(OB﹣3)2≥0,
∴OA=4,OB=3.
(2)如图2中,作DE⊥y轴于E.

∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAE+∠BAO=90°,∠DAE+∠ADE=90°,
∴∠BAO=∠ADE,
∵∠DEA=∠AOB=90°,
∴△AOB≌△DEA(AAS),
∴DE=OA=4,AE=OB=3,
∴OE=7,
∴点D坐标为(4,7).
(3)存在.在Rt△AOB中,AB=![]() =5,
=5,
∴当PA=AB=5时,P(0,9)或(0,﹣1),
当PB=BA时,P(0,﹣4).

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目