��Ŀ����
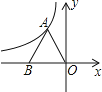
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����x�ύ�ڵ�A����1��0������y�ύ�ڵ�B���ҶԳ���Ϊx=1����������ĸ����ۣ�
�ٵ�x����1ʱ��y��0��
��һԪ���η���ax2+bx+c=0������Ϊx1=��1��x2=3��
�۵�y��0ʱ��x����1��
�������������㣨x1��y1������x2��y2������x1��x2��2ʱ��y1��y2
������ȷ���۵ĸ����ǣ�������

A. 3 B. 2 C. 1 D. 0
���𰸡�B
��������
ֱ�����ö��κ����ĶԳ��Եó�ͼ����x�����һ������������ͼ�η���������
�߶��κ���y=ax2+bx+c��a��0���IJ���ͼ����x�ύ�ڵ�A����1��0������y�ύ�ڵ�B���ҶԳ���Ϊx=1����ͼ����x�����һ������Ϊ����3��0�����ʢٵ�3��x����1ʱ��y��0���ʴ�ѡ�������
��һԪ���η���ax2+bx+c=0������Ϊx1=��1��x2=3����ȷ��
�۵�y��0ʱ��x����1��x��3���ʴ�ѡ�������
�������������㣨x1��y1������x2��y2������x1��x2��2ʱ�����㶼�ڶԳ����Ҳ���y��x���������С����y1��y2���ʴ�ѡ����ȷ��
��ѡB��

��ϰ��ϵ�д�
 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
�����Ŀ