题目内容
【题目】如图，AB为⊙O的直径，C、D是⊙O上的点，且OC∥BD，AD分别与BC、OC相交于 点E、F．若∠CBD=36°，则下列结论中不正确的是
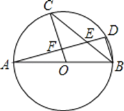
A. ∠AOC=72° B. ∠AEC=72° C. AF=DF D. BD=20F
【答案】B
【解析】
根据平行线的性质和三角形外角的性质可判断A正确，再根据圆周角定理和三角形内角和定理及对顶角相等可知∠AEC=54°，然后根据中位线的性质可知C、D正确.
∵OC∥BD，
∴∠OCB=∠CBD=36°.
∵OB=OC，
∴∠OBC=∠OCB=36°，
∴∠AOC=72°.
故A正确.
∵AB为直径，
∴∠ADB=90°.
∴∠AEC=∠BED=54°.
故B错误.
∵OC∥BD，且OA=OB，
∴OF是△ABD的中位线，
∴AF=DF，BD=20F.
故C、D正确.
故选B.
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
