题目内容
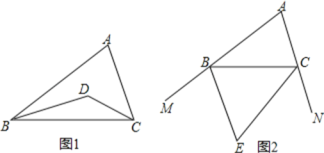
【题目】(1)如图1,在△ABC中,BD、CD分别是△ABC两个内角∠ABC、∠ACB的平分线.
①若∠A=70°,求∠BDC的度数.
②∠A=α,请用含有α的代数式表示∠BDC的度数.(直接写出答案)
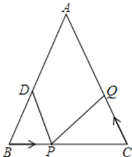
(2)如图2,BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线.若∠A=α,请用含有α的代数式表示∠BEC的度数.
【答案】(1)①125°;②∠A=90°+![]() α;(2)∠BEC=90°﹣
α;(2)∠BEC=90°﹣![]() α.
α.
【解析】
(1)①根据角平分线定义可得到∠ABD=∠CBD,∠BCD=∠ACD,再根据三角形内角和定理得到∠DBC+∠BCD+∠BDC=180°,∠ABD+∠CBD+∠BCD+∠ACD+∠A=180°,利用等量代换可得2(180°﹣∠BDC)+∠A=180°,进而得到∠BDC=90°+![]() ∠A;②直接利用①的结论写出即可
∠A;②直接利用①的结论写出即可
(2)利用角平分线定义得到∠EBC=![]() ∠MBC,∠BCE=
∠MBC,∠BCE=![]() ∠BCM,再由三角形外角性质得到∠CBM+∠BCN=360°﹣(180°﹣∠A)=180°+∠A,进而得∠EBC+∠BCE=
∠BCM,再由三角形外角性质得到∠CBM+∠BCN=360°﹣(180°﹣∠A)=180°+∠A,进而得∠EBC+∠BCE=![]() (∠MBC+∠BCN)=
(∠MBC+∠BCN)=![]() (180°+∠A)=90°+
(180°+∠A)=90°+![]() ∠A,再在△DBC中利用内角和定理得到∠BEC=180°﹣(∠EBC+∠BCE),进行化简即可得到结论.
∠A,再在△DBC中利用内角和定理得到∠BEC=180°﹣(∠EBC+∠BCE),进行化简即可得到结论.
解:(1)①∵∠ABC,∠ACB的平分线相交于点D,
∴∠ABD=∠CBD,∠BCD=∠ACD,
∵∠DBC+∠BCD+∠BDC=180°,∠ABD+∠CBD+∠BCD+∠ACD+∠A=180°,
∴2∠DBC+2∠BCD+∠A=180°,
∴2(180°﹣∠BDC)+∠A=180°,
∴∠BDC=90°+![]() ∠A,
∠A,
∵∠A=70°,
∴∠BDC=90°+![]() ×70°=90°+35°=125°.
×70°=90°+35°=125°.
②利用①得到的∠BDC=90°+![]() ∠A,直接表示出∠BDC=90°+
∠A,直接表示出∠BDC=90°+![]() α.
α.
(2)∵BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线,
∴∠EBC=![]() ∠MBC,∠BCE=
∠MBC,∠BCE=![]() ∠BCM,
∠BCM,
∵∠CBM、∠BCN是△ABC的两个外角
∴∠CBM+∠BCN=360°﹣(180°﹣∠A)=180°+∠A
∴∠EBC+∠BCE=![]() (∠MBC+∠BCN)=
(∠MBC+∠BCN)=![]() (180°+∠A)=90°+
(180°+∠A)=90°+![]() ∠A,
∠A,
在△DBC中,
∵∠BEC=180°﹣(∠EBC+∠BCE)
=180°﹣(90°+![]() ∠A)
∠A)
=90°﹣![]() ∠A,且∠A=α,
∠A,且∠A=α,
∴∠BEC=90°﹣![]() α.
α.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案