题目内容
【题目】某中学为了解九年级学生对三大球类运动的喜爱情况,从九年级学生中随机抽取部分学生进行调查问卷,通过分析整理绘制了如下两幅统计图.请根据两幅统计图中的信息回答下列问题:

(1)求参与调查的学生中,喜爱排球运动的学生人数,并补全条形图;
(2)若该中学九年级共有800名学生,请你估计该中学九年级学生中喜爱篮求运动的学生有多少名?
(3)若从喜爱足球运动的2名男生和2名女生中随机抽取2名学生,确定为该校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.
【答案】(1)60,补全图见解析;(2)360;(3)![]()
【解析】
(1)首先求出总人数,进而可求出喜爱排球运动的学生人数,并补全条形图即可;
(2)由总人数乘以喜爱篮球运动的学生的百分数即可得解;
(3)画树状图展示12种等可能的结果数,再找出抽取的两人恰好是一名男生和一名女生结果数,然后根据概率公式求解.
解:(1)由题意可知调查的总人数=12÷20%=60(人),
所以喜爱排球运动的学生人数=60×35%=21(人)
补全条形图如图所示: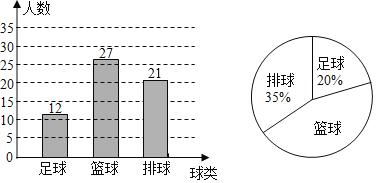
(2)∵该中学九年级共有800名学生,
∴该中学九年级学生中喜爱篮球运动的学生有800×(1-35%-20%)=360名;
(3)画树状图为:
共有12种等可能的结果数,其中抽取的两人恰好是一名男生和一名女生结果数为8,
所以抽取的两人恰好是一名男生和一名女生概率=![]() .
.

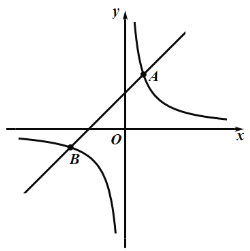
【题目】如图:反比例函数 与一次函数 的图象交于A(1,3)和B(-3,n)两点.
(1)求反比例函数与一次函数的解析式;
(2)当x取什么值时,一次函数的值大于反比例函数的值.
(3)求出△OAB的面积.
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) | x60 | x |
售价(元/件) | 200 | 100 |
若用1800元购进甲种商品的件数与用900元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共100件,其中销售甲种商品为a件(a40),设销售完100件甲、乙两种商品的总利润为w元,求w与a之间的函数关系式,并求出w的最小值.