题目内容
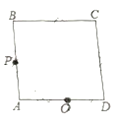
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N. 连接PB,在点P运动过程中,PM+PN+PB的最小值等于_________ .

【答案】7.8
【解析】
在△ADO中,由勾股定理可求得AD=5,由AC⊥BD,AO=CO,可知DO是AC的垂直平分线,由线段垂直平分线的性质可知AD=DC;利用面积法可证得PM+PN为定值,当PB最短时,PM+PN+PB有最小值,由垂线的性质可知当点P与点O重合时,OB有最小值.
∵AC⊥BD于点O,AO=CO=4,BO=DO=3,
∴在Rt△AOD中,
AD=![]() ,
,
∵AC⊥BD于点O,AO=CO,
∴CD=AD=5,
如图所示:连接PD,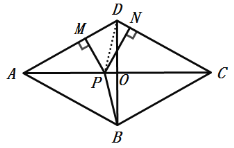
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴PM+PN=4.8,
∴当PB最短时,PM+PN+PB有最小值,
∵由垂线段最短可知:当BP⊥AC时,PB最短.
∴当点P与点O重合时,PM+PN+PB有最小,最小值=![]() .
.
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】随着高铁的建设,春运期间动车组发送旅客量越来越大,相关部门为了进一步了解春运期间动车组发送旅客量的变化情况,针对2014年至2018年春运期间的铁路发送旅客量情况进行了调查,过程如下.
(Ⅰ)收集、整理数据
请将表格补充完整:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
动车组发送旅客量a亿人次 | 0.87 | 1.14 | 1.46 | 1.80 | 2.17 |
铁路发送旅客总量b亿人次 | 2.52 | 2.76 | 3.07 | 3.42 | 3.82 |
动车组发送旅客量占比 | 34.5% | 41.3% | 47.6% | 52.6% |
(Ⅱ)描述数据
为了更直观地显示动车组发送旅客量占比的变化趋势,需要用 (填“折线图”或“扇形图”)进行描述;
(Ⅲ)分析数据、做出推测
预估2019年春运期间动车组发送旅客量占比约为 ,你的预估理由是 .