题目内容
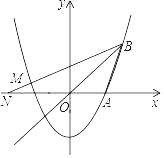
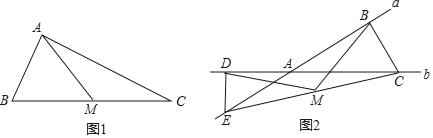
【题目】(1)如图1,在△ABC中,点M为BC边的中点,且MA=![]() BC,求证:∠BAC=90°.
BC,求证:∠BAC=90°.
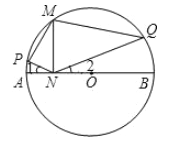
(2)如图2,直线a、b相交于点A,点C、E分别是直线b、a上两点,ED⊥b,垂足为点D,点M是EC的中点,MD=MB,DE=2,BC=3,求△ADE和△ABC的面积之比.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据点M为BC的中点,得到BM=CM=![]() BC.又MA=
BC.又MA=![]() BC,根据等量代换得到BM=CM=MA,根据等边对等角有∠BAM=∠B,∠CAM=∠C,又∠BAM+∠B+∠CAM+∠C=180°,即可得到∠BAM+∠CAM=90°,即可证明.
BC,根据等量代换得到BM=CM=MA,根据等边对等角有∠BAM=∠B,∠CAM=∠C,又∠BAM+∠B+∠CAM+∠C=180°,即可得到∠BAM+∠CAM=90°,即可证明.
(2)根据(1)的结论,可得∠EBC=90°,即可证明△ADE∽△ABC,根据相似三角形的性质即可解答.
(1)证明:∵点M为BC的中点,
∴BM=CM=![]() BC.
BC.
∵MA=![]() BC,
BC,
∴BM=CM=MA,
∴∠BAM=∠B,∠CAM=∠C,
∴∠BAM+∠B+∠CAM+∠C=180°,
∴2∠BAM+2∠CAM=180°,
∴∠BAM+∠CAM=90°,即∠BAC=90°.
(2)解:∵点M为EC的中点,ED⊥AC于点D,
∴DM=![]() EC.
EC.
∵BM=DM,
∴BM=![]() EC,
EC,
∴∠EBC=90°.
∴∠ADE=∠ABC=90°.
又∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴![]()

练习册系列答案
相关题目