题目内容
【题目】如图，
是⊙
的直径，
是⊙上一点，
，垂足为
、
、
分别是
、
上一点（不与端点重合），如果
，下面结论：①
；②
；③
；④
；⑤
．其中正确的是（ ）
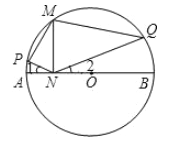
A. ①②③B. ①③⑤C. ④⑤D. ①②⑤
【答案】B
【解析】
利用等角的余角相等得到①对；利用三角形内角和定理得②错；利用垂径定理，同弧所对的圆周角相等得③对；利用三角形相似得④错，⑤对．
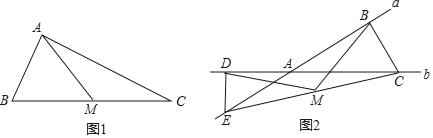
解：延长QN交圆O于C，延长MN交圆O于D，如图
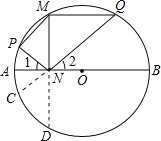
∵MN⊥AB，∠MNP=∠MNQ，
则∠1=∠2，故①正确；
∵∠P+∠PMN＜180°，
∴∠P+∠Q＜180°，故②错误；
∵AB是⊙O的直径，MN⊥AB，
，
由∠1=∠2，∠ANC=∠2，
∴∠1=∠ANC，
得P，C关于AB对称，
，
，
∴∠Q=∠PMN，故③正确；
∵∠MNP=∠MNQ，∠Q=∠PMN，
∴△PMN∽△MQN，
∴MN2=PNQN，PM不一定等于MQ；
故④错误，⑤正确．
故选：B．
练习册系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
【题目】盒中有若干枚黑棋和白棋，这些棋除颜色外无其他差别，现让学生进行摸棋试验：每次摸出一枚棋，记录颜色后放回摇匀．重复进行这样的试验得到以下数据：
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
（1）根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ；（精确到0.01）
（2）若盒中黑棋与白棋共有4枚，某同学一次摸出两枚棋，请计算这两枚棋颜色不同的概率，并说明理由
