题目内容
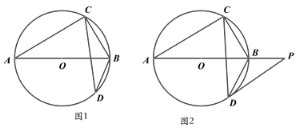
【题目】如图,AB是半圆O的直径,点P(不与点A,B重合)为半圆上一点,将图形沿BP折叠,分别得到点A,O的对应点点A′,O′,过点A′C∥AB,若A′C与半圆O恰好相切,则∠ABP的大小为_____°.
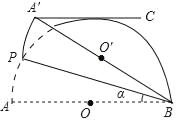
【答案】15
【解析】
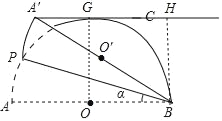
作OG⊥A′C于G,BH⊥A′C于H,如图,根据切线的性质得到OG=OB,再利用A′C∥AB可证明四边形OBHG为正方形,接着根据折叠的性质得∠A′BP=∠ABP=α,BA′=BA,所以A′B=2BH,根据特殊角的三角函数值得到∠BA′H=30°,然后利用∠HA′B=∠ABA′=2α可确定α的度数.
作OG⊥A′C于G,BH⊥A′C于H,如图,
∵A′C与半圆O恰好相切,
∴OG为⊙O的半径,即OG=OB,
∵A′C∥AB,
∴OG⊥OB,BH⊥OB,∠HA′B=∠ABA′,
∴四边形OBHG为正方形,
∵图形沿BP折叠,分别得到点A,O的对应点点A′,O′,
∴∠A′BP=∠ABP=α,BA′=BA,
∴A′B=2BH,
∴∠BA′H=30°,
∵∠HA′B=∠ABA′=2α,
∴α=15°,
故答案为:15.

练习册系列答案
相关题目