题目内容
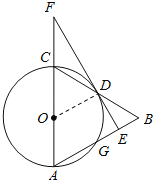
【题目】如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
(1)求证:直线EF是⊙O的切线;
(2)若CF=3,cosA=0.4,求出⊙O的半径和BE的长;
(3)连接CG,在(2)的条件下,求CG:EF的值.

【答案】(1)见解析;(2)2,![]() (3)CG:EF=4:7
(3)CG:EF=4:7
【解析】试题分析:(1)连结OD.先证明OD是△ABC的中位线,根据中位线的性质得到OD∥AB,再由DE⊥AB,得出OD⊥EF,根据切线的判定即可得出直线EF是⊙O的切线;
(2)先由OD∥AB,得出∠COD=∠A,再解Rt△DOF,根据余弦函数的定义得到cos∠FOD=![]() =
=![]() ,设⊙O的半径为R,解方程
,设⊙O的半径为R,解方程![]() =
=![]() ,求出R=
,求出R=![]() ,那么AB=2OD=
,那么AB=2OD=![]() ,解Rt△AEF,根据余弦函数的定义得到cosA=
,解Rt△AEF,根据余弦函数的定义得到cosA=![]() =
=![]() ,求出AE=
,求出AE=![]() ,然后由BE=AB﹣AE即可求解.
,然后由BE=AB﹣AE即可求解.
试题解析:
(1)证明:如图,连结OD.
∵CD=DB,CO=OA,
∴OD是△ABC的中位线,
∴OD∥AB,AB=2OD,
∵DE⊥AB,
∴DE⊥OD,即OD⊥EF,
∴直线EF是⊙O的切线;
(2)解:∵OD∥AB,
∴∠COD=∠A.
在Rt△DOF中,∵∠ODF=90°,
∴cos∠FOD=![]() =
=![]() ,
,
设⊙O的半径为R,则![]() =
=![]() ,
,
解得R=![]() ,
,
∴AB=2OD=![]() .
.
在Rt△AEF中,∵∠AEF=90°,
∴cosA=![]() =
=![]() =
=![]() ,
,
∴AE=![]() ,
,
∴BE=AB﹣AE=![]() ﹣
﹣![]() =2.
=2.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
【题目】某公园门票的收费标准如下:
门票类别 | 成人票 | 儿童票 | 团体票(限5张及以上) |
价格(元/人) | 100 | 40 | 60 |
有两个家庭分别去该公园游玩,每个家庭都有5名成员,且他们都选择了最省钱的方案购买门票,结果一家比另一家少花40元,则花费较少的一家花了_____元.
