题目内容
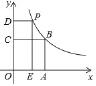
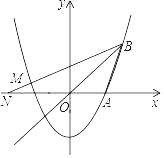
【题目】如图,抛物线y=![]() x2+bx+c过点A(2,0)和B(3,3).
x2+bx+c过点A(2,0)和B(3,3).
(1)求抛物线的表达式;
(2)点M在第二象限的抛物线上,且∠MBO=∠ABO.
①直线BM交x轴于点N,求线段ON的长;
②延长BO交抛物线于点C,点P是平面内一点,连接PC、OP,当△POC∽△MOB时,请直接写出点P的坐标.
【答案】(1)![]() ;(2)①ON=6;②点P坐标为
;(2)①ON=6;②点P坐标为![]() 或
或![]()
【解析】
(1)把点A、B坐标代入二次函数表达式,即可求解;
(2)①证明△BOL≌△BOA,利用![]() 即可求解;②当△POC∽△MOB时,点P的位置可能第二象限也可能在第四象限,分别求解即可.
即可求解;②当△POC∽△MOB时,点P的位置可能第二象限也可能在第四象限,分别求解即可.
解:(1)把点A、B坐标代入二次函数表达式:
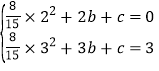 ,解得:
,解得: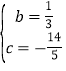 ,
,
故:抛物线的表达式为:![]() ……①;
……①;
(2)①过点B分别向x轴、y轴作垂线,交于点S、K,连接A、L,
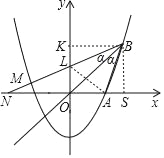
点B坐标为(3,3)则:四边形OSBK为正方形,
∵∠MBO=∠ABO,BO是正方形OSBK的对角线,BO=BO,
∴△BOL≌△BOA(AAS),
∴OA=OL=2,∴AL⊥BO,
sinα=![]() =
=![]() =
=![]() ,则cosα=
,则cosα=![]() ,tanα=
,tanα=![]() ,
,
∵OL∥BS,∴![]() ,即:
,即:![]() ,
,
则:ON=6;
②则点N坐标为(﹣6,0),
把点L(0,2)、N坐标代入一次函数表达式:y=kx+b,
解得:y=![]() x+2…②,
x+2…②,
联立①、②解得:x=﹣3或3(舍去3)
即点M坐标为(﹣3,1),
BC所在的直线的表达式为:y=x…③,
联立①、③解得:x=﹣![]() 或3(舍去3),
或3(舍去3),
则点C坐标为(﹣![]() ,﹣
,﹣![]() ),
),
则:OM=![]() ,OB=3
,OB=3![]() ,OC=
,OC=![]() ,MB=2
,MB=2![]()
当△POC∽△MOB时,点P的位置可能第二象限也可能在第四象限,
当点P在第二象限时,如下图,过点P作PH⊥x轴,
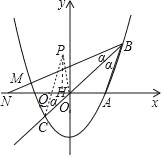
△POC∽△MOB,∠PCO=∠MBO=α,
∴![]() =
=![]() =
=![]() ,即:
,即:![]() =
=![]() ,
,
解得:OP=![]()
![]() ,PC═
,PC═![]() ,
,
AB所在直线表达式中的k值为3,
∵∠PCO=∠MBO=∠OBA=α,
∴PC所在直线表达式中的k值为3,
则:PC所在的直线表达式为:y=3x+![]() ,
,
令y=0,则x=﹣![]() ,
,
即Q点坐标为(﹣![]() ,0),即:OQ=
,0),即:OQ=![]() ,
,
则:CQ=![]()
![]() ,则:PQ=PC﹣CQ,
,则:PQ=PC﹣CQ,
而PH2=OP2﹣OH2=PQ2﹣QH2=PQ2﹣(OQ﹣OH)2,
其中,OP=![]()
![]() ,PQ=PC﹣CQ,OQ=
,PQ=PC﹣CQ,OQ=![]() ,
,
解得:OH=![]() ,
,
则点P坐标为(﹣![]() ,
,![]() ),
),
当点P在第四象限时,同理可求点P坐标为![]() ,
,
故点P坐标为![]() 或
或![]() .
.

【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由