��Ŀ����
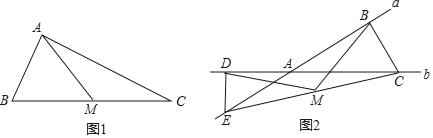
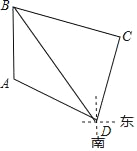
����Ŀ���ֱ�ֹ��A��B����B��A�������������ҹ����Ҿ������10km��Ϊ��D����һ���ҹ�����ִ�л�������A���������D������ƫ��63.4�㣬B���������D������ƫ��36.8�㣮�������ű�ƫ��16.4�㷽������12km����C�㣬��ʱ��B���ľ������C������ƫ��73.6�㷽���ϣ�
��1�����BCD�Ķ�����
��2����AD�ij������ο����ݣ�sin36.8���0.60��cos36.8���0.80��tan26.6���0.50��![]() ��2.24��
��2.24��
���𰸡���1����BCD��90�㣻��2��AD��13.44km��
��������
��1������DCF�������������ڽǺͶ������ɽ�����⣻
��2����DE��BA��BA���ӳ�����E����tan26.6����![]() ��0.5����AE��x����DE��2x����Rt��DEB�У�tan36.8����
��0.5����AE��x����DE��2x����Rt��DEB�У�tan36.8����![]() ���ɵ�
���ɵ�![]() �����x���ɽ�����⣻
�����x���ɽ�����⣻
��1���ߡ�DFC����ABC��73.6������CDF��16.4����
���BCD��180����73.6����16.4����90����
��2����DE��BA��BA���ӳ�����E��

��Rt��AED��tan��ADE��![]() ��
��
��tan26.6����![]() ��0.5����AE��x����DE��2x��
��0.5����AE��x����DE��2x��
��Rt��DEB��tan36.8����![]() ��
��
��![]() ��
��
��x��6��
��AD��![]() =
=![]() x��6��2.24��13.44km��
x��6��2.24��13.44km��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ������������ö����Ͱ��壬��Щ�����ɫ���������������ѧ�������������飺ÿ������һö�壬��¼��ɫ��Ż�ҡ�ȣ��ظ���������������õ��������ݣ�
����Ĵ���n | 100 | 200 | 300 | 500 | 800 | 1000 |
��������Ĵ���m | 24 | 51 | 76 | 124 | 201 | 250 |
���������Ƶ�� | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
��1�����ݱ������ݹ��ƴӺ�������һö���Ǻ���ĸ������� ��������ȷ��0.01��
��2�������к�������干��4ö��ijͬѧһ��������ö�壬���������ö����ɫ��ͬ�ĸ��ʣ���˵������