题目内容
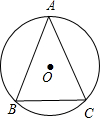
如图，AB为半圆的直径，C为半圆上一点，CD⊥AB于D．若CD=6，AD：DB=3：2，则AC•BC等于（ ）
A．15
| B．30
| C．60
| D．90 |
∵AB为半圆的直径，
∴∠ACB=90°，
又∵CD⊥AB，
∴△ADC∽△CDB，
∴CD2=AD•BD，而CD=6，AD：DB=3：2，可设AD=3x，BD=2x，
所以36=2x•3x，则x=
，
∴AD=3
，BD=2
，
再利用勾股定理，得AC=3
，BC=2
，
所以AC•BC=3
×2
=30
．
故选B．
∴∠ACB=90°，
又∵CD⊥AB，
∴△ADC∽△CDB，
∴CD2=AD•BD，而CD=6，AD：DB=3：2，可设AD=3x，BD=2x，
所以36=2x•3x，则x=
| 6 |
∴AD=3
| 6 |
| 6 |
再利用勾股定理，得AC=3
| 10 |
| 15 |
所以AC•BC=3
| 10 |
| 15 |
| 6 |
故选B．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
