题目内容
如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.

(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
(3)若∠EAB=30°,CF=2,求GA的长.

(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
(3)若∠EAB=30°,CF=2,求GA的长.
(1)连接OC,由C是劣弧AE的中点,根据垂径定理得OC⊥AE,而CG∥AE,所以CG⊥OC,然后根据切线的判定定理即可得到结论。
(2)连接AC、BC,根据圆周角定理得∠ACB=90°,∠B=∠1,而CD⊥AB,则∠CDB=90°,根据等角的余角相等得到∠B=∠2,所以∠1=∠2,于是得到AF=CF。
(3)2
(2)连接AC、BC,根据圆周角定理得∠ACB=90°,∠B=∠1,而CD⊥AB,则∠CDB=90°,根据等角的余角相等得到∠B=∠2,所以∠1=∠2,于是得到AF=CF。
(3)2

分析:(1)连接OC,由C是劣弧AE的中点,根据垂径定理得OC⊥AE,而CG∥AE,所以CG⊥OC,然后根据切线的判定定理即可得到结论。
(2)连接AC、BC,根据圆周角定理得∠ACB=90°,∠B=∠1,而CD⊥AB,则∠CDB=90°,根据等角的余角相等得到∠B=∠2,所以∠1=∠2,于是得到AF=CF。
(3)在Rt△ADF中,由于∠DAF=30°,FA=FC=2,根据含30度的直角三角形三边的关系得到DF=1,AD=
 ,再由AF∥CG,根据平行线分线段成比例得到DA:AG=DF:CF然后把DF=1,AD=
,再由AF∥CG,根据平行线分线段成比例得到DA:AG=DF:CF然后把DF=1,AD= ,CF=2代入计算即可。
,CF=2代入计算即可。解:(1)证明:如图,连接OC,
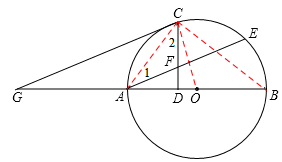
∵C是劣弧AE的中点,∴OC⊥AE。
∵CG∥AE,∴CG⊥OC。
∵OC是⊙O的半径,∴CG是⊙O的切线。
(2)证明:连接AC、BC,
∵AB是⊙O的直径,∴∠ACB=90°。
∴∠2+∠BCD=90°。
∵CD⊥AB,∴∠B+∠BCD=90°。∴∠B=∠2。
∵AC弧=CE弧,∴∠1=∠B。
∴∠1=∠2。∴AF=CF。
(3)在Rt△ADF中,∠DAF=30°,FA=FC=2,∴DF=
 AF=1。
AF=1。∴AD=
 DF=
DF= 。
。∵AF∥CG,∴DA:AG=DF:CF,即
 :AG=1:2。
:AG=1:2。∴AG=2
 。
。
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目

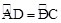

 与
与 互为倒数
互为倒数