题目内容
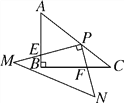
【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求EE′的长?并求出∠BE′C的度数?
【答案】![]() 135°
135°
【解析】
首先根据旋转的性质得出,△EBE′是直角三角形,得到EE′=![]() BE,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
BE,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
解:连接EE′,如图,
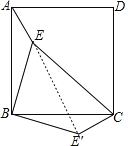
∵△ABE绕点B顺时针旋转90°得到△CBE′,
∴BE=BE′=2,AE=CE′=1,∠EBE′=90°,
∴△BEE′为等腰直角三角形,
∴EE′=![]() BE=2
BE=2![]() ,∠BE′E=45°,
,∠BE′E=45°,
在△CEE′中,CE=3,CE′=1,EE′=2![]() ,
,
∵12+(2![]() )2=32,
)2=32,
∴CE′2+EE′2=CE2,
∴△CEE′为直角三角形,
∴∠EE′C=90°,
∴∠BE′C=∠BE′E+∠CE′E=135°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】小洋八年级下学期的数学成绩(单位:分)如下表所示:
测试 类别 | 平时 | 期中 考试 | 期末 考试 | |||
测验1 | 测验2 | 测验3 | 测验4 | |||
成绩 | 106 | 102 | 115 | 109 | 112 | 110 |
(1)计算小洋该学期的数学平时平均成绩;
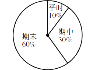
(2)如果该学期的总评成绩是根据如图所示的权重计算的,请计算出小洋该学期的数学总评成绩.