Question

【题目】将一副分别含有30°和45°角的两个三角板的直角顶点C叠放在一起．

①如图，CD平分∠ECB，求∠ACB与∠DCE的和．

②如图，若CD不平分∠ECB，请你直接写出∠ACB与∠DCE之间所具有的数量关系(不要求说出理由)．

Answer 1

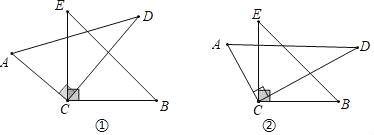
【答案】①∠ACB+∠DCE＝180°；②∠ACB+∠DCE＝180°.

【解析】

①根据角平分线的定义求出∠BCD＝∠DCE＝45°，然后根据角的和差即可得到结论；

②根据∠ACB+∠DCE＝90°+∠BCD+∠DCE即可得到结论．

解：①∵CD平分∠ECB，∠ACD＝∠BCE＝90°，

∴∠BCD＝∠DCE＝45°，

∴∠ACB+∠DCE＝90°+45°+45°＝180°；

②∵∠ACD＝∠BCE＝90°，

∴∠ECD+∠DCB＝90°，

∴∠ACB+∠DCE＝90°+∠BCD+∠DCE＝90°+90°＝180°．