��Ŀ����
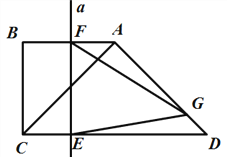
����Ŀ������ǡ�ABC�У�AB=4��BC=5����ACB=45�㣬����ABC�Ƶ�B����ʱ�뷽����ת���õ� ��A1BC1��
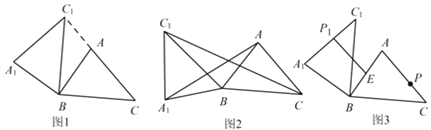
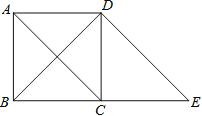
��1����ͼ1������C1���߶�CA���ӳ�����ʱ�����CC1A1�Ķ�����
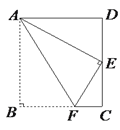
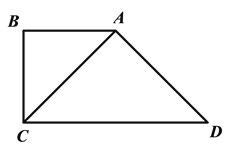
��2����ͼ2������AA1��CC1������ABA1�����Ϊ4�����CBC1�������
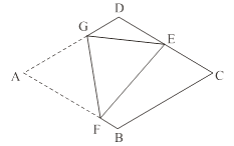
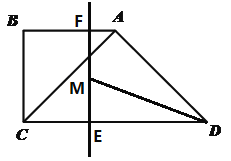
��3����ͼ3����EΪ�߶�AB�е㣬��P���߶�AC�ϵĶ��㣬�ڡ�ABC �Ƶ� B ����ʱ�뷽����ת�����У���P�Ķ�Ӧ���ǵ�P1�����߶�EP1���ȵ����ֵ����Сֵ��
���𰸡���1��90�㣻��2��![]() ����3��
����3��![]() ��7.
��7.
�������������������1������ת�����ʿɵã���A1C1B=��ACB=45����BC=BC1�����ݵȱ߶ԵȽǵõ���CC1B=��C1CB=45����������CC1A1=��CC1B+��A1C1B�ý⣻
��2��ͨ��֤����ABA1�ס�CBC1���������������ε�����ȵ������Ʊȵ�ƽ���õ��� ���ݴ˽����CBC1�������
���ݴ˽����CBC1�������
��3������B��BD��AC��DΪ���㣬���BD=![]() ������P��AC���˶��������D��ʹ��P�Ķ�Ӧ��P1���߶�AB��ʱ��EP1=BP1��BE������P��AC���˶�����C��ʹ��P�Ķ�Ӧ��P1���߶�AB���ӳ�����ʱ��EP1���EP1=BC+BE��
������P��AC���˶��������D��ʹ��P�Ķ�Ӧ��P1���߶�AB��ʱ��EP1=BP1��BE������P��AC���˶�����C��ʹ��P�Ķ�Ӧ��P1���߶�AB���ӳ�����ʱ��EP1���EP1=BC+BE��
����������⣺��1��������ת�����ʿɵã���A1C1B=��ACB=45����BC=BC1��
���CC1B=��C1CB=45����
���CC1A1=��CC1B+��A1C1B=45��+45��=90����
��2��������ת�����ʿɵã���ABC�ա�A1BC1��
��BA=BA1��BC=BC1����ABC=��A1BC1��
��![]() ����ABC+��ABC1=��A1BC1+��ABC1��
����ABC+��ABC1=��A1BC1+��ABC1��
���ABA1=��CBC1��
���ABA1�ס�CBC1��
�� ��
��
��S��ABA1=4����S��CBC1=![]() ��
��
��3������B��BD��AC��DΪ���㣬
�ߡ�ABCΪ��������Σ�����D���߶�AC�ϣ�
��Rt��BCD��BD=BC��sin45��=![]() ��
��
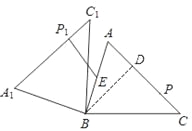
����ͼ1����P��AC���˶��������D����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB��ʱ��EP1��С����СֵΪ��EP1=BP1��BE=BD��BE=![]() ��2��
��2��
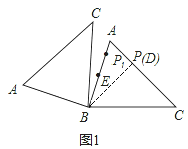
����ͼ2����P��AC���˶�����C����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB���ӳ�����ʱ��EP1������ֵΪ��EP1=BC+BE=5+2=7��

����Ŀ��ij��˾����һ�ֽ���Ϊ20Ԫ/���ļ���������������y������������ۼ۸�x��Ԫ/���� �ı仯���±���ͬʱ�����۹����е�������֧���������ۣ��ܼ�40��Ԫ��
���ۼ۸�x(Ԫ/��) | �� | 30 | 40 | 50 | 60 | �� |
������y(���) | �� | 5 | 4 | 3 | 2 | �� |
��1���۲첢�������е����ݣ�����ѧ���ĺ���֪ʶ��ֱ��д��y�� x�ĺ�������ʽ��
��2������ù�˾�������ּ������ľ�������z����Ԫ�������ۼ۸� x��Ԫ/���� �ĺ�������ʽ�����ۼ۸�Ϊ����Ԫʱ��������������ֵ�Ƕ���?
��3���ù�˾Ҫ�������ܵ���40��Ԫ�������Ϻ���ͼ��������ۼ۸� x��Ԫ/���� ��ȡֵ��Χ�������迼�������������ܴ����ۼ۸�Ӧ��Ϊ����Ԫ ?